题目内容
13.已知函数f(x)=(x-1)ex+ax2,a∈R.(Ⅰ)讨论函数f(x)的单调区间;
(Ⅱ)若f(x)有两个零点,求a的取值范围.
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)求出函数g(x)的导数,通过讨论a的范围,判断函数g(x)的单调性结合函数零点的个数确定a的范围即可.
解答 解:(Ⅰ)f(x)=(x-1)ex+ax2,
f′(x)=x(ex+2a),
①a≥0时,令f′(x)>0,解得:x>0,
令f′(x)<0,解得:x<0,
∴f(x)在(-∞,0)递减,在(0,+∞)递增;
②-$\frac{1}{2}$<a<0时,ln(-2a)<0,
令f′(x)>0,解得:x>0或x<ln(-2a),
令f′(x)<0,解得:ln(-2a)<x<0,
故f(x)在(-∞,ln(-2a))递减,在(ln(-2a),0)递增,在(0,+∞)递减;
③a=-$\frac{1}{2}$时,ln1=0,f(x)在R递增;
④a<-$\frac{1}{2}$时,ln(-2a)>0,
令f′(x)>0,解得:x<0或x>ln(-2a),
令f′(x)<0,解得:ln(-2a)>x>0,
故f(x)在(-∞,0)递减,在(0,ln(-2a))递增,在(ln(-2a),+∞)递减;
(Ⅱ)函数g(x)的定义域为R,由已知得g'(x)=x(ex+2a).
①当a=0时,函数g(x)=(x-1)ex只有一个零点;
②当a>0,因为ex+2a>0,
当x∈(-∞,0)时,g'(x)<0;当x∈(0,+∞)时,g'(x)>0.
所以函数g(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增.
又g(0)=-1,g(1)=a,
因为x<0,所以x-1<0,ex<1,所以ex(x-1)>x-1,所以g(x)>ax2+x-1,
取x0=$\frac{-1-\sqrt{1+4a}}{2a}$,显然x0<0且g(x0)>0,
所以g(0)g(1)<0,g(x0)g(0)<0,
由零点存在性定理及函数的单调性知,函数有两个零点.
③当a<0时,由g'(x)=x(ex+2a)=0,得x=0,或x=ln(-2a).
ⅰ) 当a<-$\frac{1}{2}$,则ln(-2a)>0.
当x变化时,g'(x),g(x)变化情况如下表:
| x | (-∞,0) | 0 | (0,ln(-2a)) | ln(-2a) | (ln(-2a),+∞) |
| g'(x) | + | 0 | - | 0 | + |
| g(x) | ↗ | -1 | ↘ | ↗ |
ⅱ) 当a=-$\frac{1}{2}$,则ln(-2a)=0,g(x)在(-∞,+∞)单调递增,函数g(x)至多有一个零点,不符合题意.
若a>-$\frac{1}{2}$,则ln(-2a)≤0.
当x变化时,g'(x),g(x)变化情况如下表:
| x | (-∞,ln(-2a)) | ln(-2a) | (ln(-2a),0) | 0 | (0,+∞) |
| g'(x) | + | 0 | - | 0 | + |
| g(x) | ↗ | ↘ | -1 | ↗ |
综上,a的取值范围是(0,+∞).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道综合题.

| A. | -$\frac{3}{4}$ | B. | -1 | C. | $\frac{3}{2}$ | D. | 2 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | |$\overrightarrow{a}$|=1⇒$\overrightarrow{a}$=±1 | B. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$|且$\overrightarrow{a}$∥$\overrightarrow{b}$⇒$\overrightarrow{a}$=$\overrightarrow{b}$ | C. | $\overrightarrow{a}$=$\overrightarrow{b}$⇒$\overrightarrow{a}$∥$\overrightarrow{b}$ | D. | $\overrightarrow{a}$∥$\overrightarrow{0}$⇒|$\overrightarrow{a}$|=0 |
| A. | $({-2,\frac{1}{2}})$ | B. | $({-\frac{1}{2},2})$ | C. | (-∞,-2) | D. | $({\frac{1}{2},+∞})$ |
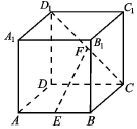 正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.
正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.