题目内容
14.四棱锥P-ABCD的底面是边长为$2\sqrt{2}$的正方形,高为1,其外接球半径为$2\sqrt{2}$,则正方形ABCD的中心与点P之间的距离为2$\sqrt{2}$.分析 由题意可知ABCD 是小圆,对角线长为4,四棱锥的高为1,推出球心O到平面ABCD的距离为2,O到PE的距离为$\sqrt{7}$,然后利用勾股定理求出底面ABCD的中心与顶点P之间的距离.
解答 解:由题意可知ABCD 是小圆,对角线长为4,四棱锥的高为1,
点P,A,B,C,D均在半径为2$\sqrt{2}$的同一球面上,
所以球心O到平面ABCD的距离为2,
设PE⊥平面ABCD,O到PE的距离为d,则d=$\sqrt{8-(2-1)^{2}}$=$\sqrt{7}$,
∴底面ABCD的中心与顶点P之间的距离为$\sqrt{7+1}$=2$\sqrt{2}$,
故答案为$2\sqrt{2}$.
点评 本题是中档题,考查球的内接多面体的知识,考查逻辑推理能力,计算能力.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
7.圆C经过直线x+y-1=0与x2+y2=4的交点,且圆C的圆心为(-2,-2),则过点(2,4)向圆C作切线,所得切线方程为( )
| A. | 5x-12y+38=0 | B. | 5x+12y+38=0 | ||
| C. | 5x-12y+38=0或x=2 | D. | 5x+12y+38=0或x=4 |
19.已知函数f(x)=cosωx+$\sqrt{3}$cosωx(ω>0),如果存在实数x0,使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2016π)成立,则ω的最小值为( )
| A. | $\frac{1}{4032π}$ | B. | $\frac{1}{2016π}$ | C. | $\frac{1}{4032}$ | D. | $\frac{1}{2016}$ |
2.某几何体的三视图如图所示,其则该几何体的体积是( )
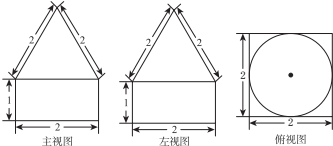

| A. | $2+\frac{{\sqrt{3}}}{3}π$ | B. | $4+\sqrt{3}π$ | C. | $\frac{4}{3}+\frac{{\sqrt{3}}}{3}π$ | D. | $4+\frac{{\sqrt{3}}}{3}π$ |
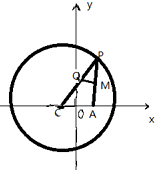 已知点C为圆(x+1)2+y2=8的圆心,P是圆上的动点,点Q在圆的半径CP上,且有点A(1,0)和AP上的点M,满足$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$.
已知点C为圆(x+1)2+y2=8的圆心,P是圆上的动点,点Q在圆的半径CP上,且有点A(1,0)和AP上的点M,满足$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$. 某单位拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).
某单位拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).