题目内容
6.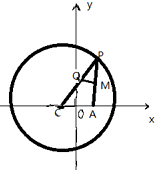 已知点C为圆(x+1)2+y2=8的圆心,P是圆上的动点,点Q在圆的半径CP上,且有点A(1,0)和AP上的点M,满足$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$.
已知点C为圆(x+1)2+y2=8的圆心,P是圆上的动点,点Q在圆的半径CP上,且有点A(1,0)和AP上的点M,满足$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$.(1)当点P在圆上运动时,求点Q的轨迹方程;
(2)若直线y=kx+$\sqrt{{k}^{2}+1}$,(k>0)与(1)中所求点Q的轨迹交于不同的两点F,H,O是坐标原点,且$\frac{2}{3}$≤$\overrightarrow{OF}$•$\overrightarrow{OH}$≤$\frac{3}{4}$时,求k的取值范围.
分析 (1)利用线段的垂直平分线的性质、椭圆的定义即可得出.
(2)设F(x1,y1),H(x2,y2),由直线y=kx+$\sqrt{{k}^{2}+1}$,(k>0)与椭圆联立得$(2{k}^{2}+1){x}^{2}+4k\sqrt{{k}^{2}+1}x+2{k}^{2}$=0,由此利用根的判别式、韦达定理、向量数量积结合已知条件能求出k的取值范围.
解答 解:(1)由题意知MQ中线段AP的垂直平分线,
∴|CP|=|QC|+|QP|=|QC|+|QA|=2$\sqrt{2}$>|CA|=2,
∴点Q的轨迹是以点C,A为焦点,焦距为2,长轴为2$\sqrt{2}$的椭圆,b=1,
故点Q的轨迹方程是$\frac{{x}^{2}}{2}+{y}^{2}$=1.
(II)设F(x1,y1),H(x2,y2),
由直线y=kx+$\sqrt{{k}^{2}+1}$,(k>0)与椭圆联立得$(2{k}^{2}+1){x}^{2}+4k\sqrt{{k}^{2}+1}x+2{k}^{2}$=0,
△=8k2>0,x1+x2=-$\frac{4k\sqrt{{k}^{2}+1}}{2{k}^{2}+1}$,x1x2=$\frac{2{k}^{2}}{2{k}^{2}+1}$,
∴$\overrightarrow{OF}$•$\overrightarrow{OH}$=x1x2+y1y2=$\frac{{k}^{2}+1}{2{k}^{2}+1}$,
∴$\frac{2}{3}$≤$\frac{{k}^{2}+1}{2{k}^{2}+1}$≤$\frac{3}{4}$
即$\frac{1}{2}$≤k2≤1,
∵k>0,∴解得$\frac{\sqrt{2}}{2}≤k≤1$.
点评 本题考查了椭圆的标准方程及其性质、一元二次方程的根与系数的关系、数量积运算性质、不等式的解法,考查了推理能力与计算能力,属于中档题.

| 成绩(单位:分) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 数学 | 8 | 12 | 40 | 32 | 8 |
| 物理 | 7 | 18 | 40 | 29 | 6 |
(2)设数学合格一人可以赢得4小时机器人操作时间,不合格一人则减少1小时机器人操作时间;物理合格一人可以赢得5小时机器人操作时间,不合格一人则减少2小时机器人操作时间.在(1)的前提下,
(i)记X为数学一人和物理一人共同赢得的机器人操作时间(单位:小时)总和,求随机变量X的分布列和数学期望;
(ii)随机抽取4名学生,求这四名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于13小时的概率.

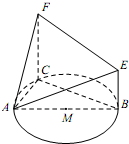 如图,某简单几何体的一个面ABC内接于圆M,AB是圆M的直径,CF∥BE,BE⊥平面ABC,且AB=2,AC=1,BE+CF=7.
如图,某简单几何体的一个面ABC内接于圆M,AB是圆M的直径,CF∥BE,BE⊥平面ABC,且AB=2,AC=1,BE+CF=7.