题目内容
设命题P:f(x)=
在区间(1,+∞)上时减函数;命题q:?a≥0,使得ax2+2x+1<0,且关于m的不等式 m2+5m-5≥a恒成立,若p∨q为真命题,p∧q为假命题,试求实数m的取值范围.
| x-m+1 |
| x-m |
考点:复合命题的真假
专题:简易逻辑
分析:分别求出命题p,q为真命题的等价条件,然后利用p∨q为真命题,p∧q为假命题,求实数m的取值范围即可.
解答:
解:对于f(x)=1+
在(m,+∞)递减,所以m≤1…(3分)
命题q:若a=0.显然成立
若a>0,则△>0得a<1,
综上0≤a<1,…(7分)
∴由m2+5m-5≥1得m≤-6或m≥1…(9分)
∵p∨q为真命题,p∧q为假命题,
∴p,q一真一假,…(10分)
∴
或
∴-6<m<1或m>1…(13分)
| 1 |
| x-m |
命题q:若a=0.显然成立
若a>0,则△>0得a<1,
综上0≤a<1,…(7分)
∴由m2+5m-5≥1得m≤-6或m≥1…(9分)
∵p∨q为真命题,p∧q为假命题,
∴p,q一真一假,…(10分)
∴
|
|
∴-6<m<1或m>1…(13分)
点评:本题主要考查全称命题和特称命题的应用以及复合命题的真假关系,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
实部为-2,虚部为1的复数所对应的点位于复平面内的( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |

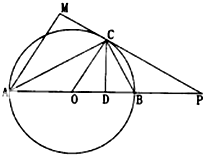 如图,已知AB是⊙O的直径,C为⊙O上一点,以C为切点的切线交AB的延长线于点P,AM⊥CP,垂足为M,CD⊥AB,垂足为D.
如图,已知AB是⊙O的直径,C为⊙O上一点,以C为切点的切线交AB的延长线于点P,AM⊥CP,垂足为M,CD⊥AB,垂足为D.