题目内容
18.在△ABC中,D是边BC的中点,|$\overrightarrow{AC}$|=3,|$\overrightarrow{AB}$|=2,则$\overrightarrow{AD}$•$\overrightarrow{BC}$=$\frac{5}{2}$.分析 由△ABC中,AB=2,AC=3,D是边BC的中点,我们易将$\overrightarrow{AD}$•$\overrightarrow{BC}$中两个向量变形为:$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$,$\overrightarrow{AD}$=$\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{AB}$,然后再利用向量数量积的计算公式,代入即可得到答案.
解答 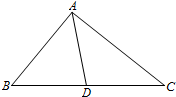 解:根据向量的加减法法则有:
解:根据向量的加减法法则有:
$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$,$\overrightarrow{AD}$=$\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{AB}$,
此时$\overrightarrow{AD}$•$\overrightarrow{BC}$=$\frac{1}{2}$($\overrightarrow{AC}$2-$\overrightarrow{AB}$2)
=$\frac{1}{2}$(9-4)
=$\frac{5}{2}$
故答案为:$\frac{5}{2}$.
点评 本题考查数量积的运算,向量在几何中的应用,考查计算能力.

练习册系列答案
相关题目
3.已知a、b、c为实常数,数列{xn}的通项xn=an2+bn+c,n∈N*,则“存在k∈N*,使得x100+k、x200+k、x300+k成等差数列”的一个必要条件是( )
| A. | a≥0 | B. | b≤0 | C. | c=0 | D. | a-2b+c=0 |
19.${∫}_{-1}^{1}$(x4tanx+x3+1)dx的值为( )
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | 0 |
20.若$z=\frac{1-i}{1+i}$(i为虚数单位)的共轭复数为( )
| A. | -1 | B. | 1 | C. | -i | D. | i |