题目内容
18.已知函数f(x)=(x-t)|x|(t∈R).(1)讨论y=f(x)的奇偶性;
(2)当t>0时,求f(x)在区间[-1,2]的最小值h(t).
分析 (1)讨论t=0和t≠0时,f(-x)与f(x)的关系,即可判断奇偶性;
(2)求出f(x)的分段形式,讨论t≥4时,0<t<4时,函数的单调性,即可得到最小值.
解答 解:(1)当t=0时,f(x)=x|x|,f(-x)=-x|-x|=-x|x|=-f(x),则f(x)为奇函数;
当t≠0时,f(-x)=(-x-t)|-x|≠±f(x),则f(x)为非奇非偶函数;
(2)$f(x)=\left\{\begin{array}{l}{x^2}-tx,x≥0\\-{x^2}+tx,x<0\end{array}\right.$.
当$\frac{t}{2}≥2$,即t≥4时,f(x)在[-1,0]上单调递增,在[0,2]上单调递减,
所以$h(x)=min\left\{{f({-1}),f({-2})}\right\}=min\left\{{-1-t,4--2t}\right\}=\left\{\begin{array}{l}-1-t,4≤t<5\\ 4-2t,t≥5\end{array}\right.$;
当$\frac{t}{2}<2$,即0<t<4时,f(x)在[-1,0]和$[{\frac{t}{2},2}]$单调递增,在$[{0,\frac{t}{2}}]$上单调递减,
所以$h(x)=min\left\{{f({-1}),f({\frac{t}{2}})}\right\}=min\left\{{-1-t,4--\frac{t^2}{4}}\right\}=-1-t$,
综上所述,h(t)=$\left\{\begin{array}{l}{-1-t,0<t<5}\\{4-2t,t≥5}\end{array}\right.$.
点评 本题考查函数的单调性和奇偶性的运用,考查分类讨论的思想方法,运算能力,属于中档题.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案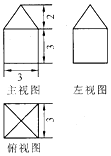
| A. | 27 | B. | 9π | C. | $\frac{27}{4}$π | D. | 33 |
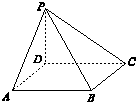 如图,在四棱锥P-ABCD中,底面ABCD是边长为m的正方形,PD⊥底面ABCD,且PD=m,PA=PC=$\sqrt{2}$m,若在这个四棱锥内放一个球,则此球的最大半径是( )
如图,在四棱锥P-ABCD中,底面ABCD是边长为m的正方形,PD⊥底面ABCD,且PD=m,PA=PC=$\sqrt{2}$m,若在这个四棱锥内放一个球,则此球的最大半径是( )| A. | $\frac{1}{3}$(2-$\sqrt{2}$)m | B. | $\frac{1}{2}$(2+$\sqrt{2}$)m | C. | $\frac{1}{2}$(2-$\sqrt{2}$)m | D. | $\frac{1}{6}$(2+$\sqrt{2}$)m |
| 偏爱蔬菜 | 偏爱肉类 | 合计 | |
| 50岁以下 | 4 | 8 | 12 |
| 50岁以上 | 16 | 2 | 18 |
| 合计 | 20 | 10 | 30 |
附:参考公式和临界值表K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 90% | B. | 95% | C. | 99% | D. | 99.9% |
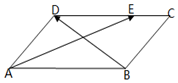 如图,在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,若$\overrightarrow{DE}=2\overrightarrow{EC}$,则$\overrightarrow{AE}•\overrightarrow{BD}$=-2.
如图,在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,若$\overrightarrow{DE}=2\overrightarrow{EC}$,则$\overrightarrow{AE}•\overrightarrow{BD}$=-2.