题目内容
20.若函数$f(x)=\frac{1}{(2x+1)(x-a)}$为偶函数,则a=( )| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
分析 根据函数奇偶性的定义建立条件关系即可得到结论.
解答 解:∵函数$f(x)=\frac{1}{(2x+1)(x-a)}$为偶函数,
∴f(-x)=f(x),
即$\frac{1}{2{x}^{2}+(2a-1)x-a}$=$\frac{1}{2{x}^{2}+(1-2a)x-a}$,
即2a-1=1-2a,
则1-2a=0,解得a=$\frac{1}{2}$,
故选D.
点评 本题主要考查函数奇偶性的判断,根据奇偶性的定义是解决本题的关键.

练习册系列答案
相关题目
10.在2和8之间插入3个数,使它们与这两个数依次构成等比数列,则这3个数的积为( )
| A. | ±64 | B. | 64 | C. | ±16 | D. | 16 |
12.设A={x|x≥2$\sqrt{2}$},a=3,下列各式正确的是( )
| A. | 0∈A | B. | a∉A | C. | a∈A | D. | {a}∈A |
9.如图是一个几何体的三视图,根据图中数据,该几何体的体积是( )
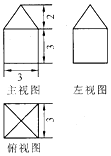

| A. | 27 | B. | 9π | C. | $\frac{27}{4}$π | D. | 33 |
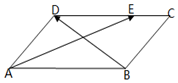 如图,在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,若$\overrightarrow{DE}=2\overrightarrow{EC}$,则$\overrightarrow{AE}•\overrightarrow{BD}$=-2.
如图,在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,若$\overrightarrow{DE}=2\overrightarrow{EC}$,则$\overrightarrow{AE}•\overrightarrow{BD}$=-2.