题目内容

16．已知是f（x）二次函数，且f（x）+f（x+1）=2x2-6x+5，求f（x）的解析式．

分析 二次函数f（x）=ax2+bx+c，代入已知式子比较系数可得abc的方程组，解方程组可得．

解答 解：设二次函数f（x）=ax2+bx+c，
则f（x）+f（x+1）=ax2+bx+c+a（x+1）2+b（x+1）+c=2x2-6x+5=2ax2+（2b+2a）x+（2c+a+b），
所以$\left\{\begin{array}{l}{2a=2}\\{2b+2a=-6}\\{a+b+2c=5}\end{array}\right.$解得a=1，b=-4，c=4，
所以f（x）=x2-4x+4．

点评 本题考查函数解析式求解的待定系数法，涉及方程组的解法，属基础题．

练习册系列答案
相关题目
6．等差数列{an}中，a3=4，a7=16，则a11=28．
7．已知椭圆C：x2+4y2=16，点M（2，1）．
（1）求椭圆C的焦点坐标和离心率；
（2）求通过M点且被这点平分的弦所在的直线方程．
4．已知函数f（x）为奇函数，且当x＞0时，$f（x）={log_{\frac{1}{3}}}$2x
（1）求当x＜0时，函数f（x）的表达式            
（2）解不等式f（x）≤3．
11．设n∈N+，由计算得f（2）=$\frac{3}{2}$，f（4）＞2，f（8）＞$\frac{5}{2}$，f（32）＞$\frac{7}{2}$，观察上述结果，可推出一般的结论为f（2n）$≥\frac{n+2}{2}$．
1．$1+11+111+…+\underbrace{11111…1}_{n个1}$之和是$\frac{{{{10}^{n+1}}-9n-10}}{81}$．
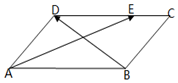8．如图，在平行四边形ABCD中，已知AB=2，AD=1，∠BAD=60°，若$\overrightarrow{DE}=2\overrightarrow{EC}$，则$\overrightarrow{AE}•\overrightarrow{BD}$=-2．
5．求值：$\frac{1}{\sqrt{2}-1}$-（$\frac{3}{5}$）0+（$\frac{9}{4}$）-0.5+$\root{4}{（\sqrt{2}-2）^{4}}$．
6．已知点（2，9）在函数f（x）=ax（a＞0且a≠1）图象上，对于函数y=f（x）定义域中的任意x1，x2（x1≠x2），有如下结论：
①f（x1+x2）=f（x1）•f（x2）；
②f（x1•x2）=f（x1）+f（x2）；
③$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＜0；
④f（$\frac{{x}_{1}+{x}_{2}}{2}$）＜$\frac{f（{x}_{1}）+f（{x}_{2}）}{2}$
上述结论中正确结论的序号是①④．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网