题目内容
已知α、β、γ是三个不重合的平面,m、n是两条不重合的直线,下列命题为真命题的是( )
| A、m∥α,n∥α,则m∥n |
| B、α∥γ,n∥β,α∩β=m,则m∥n |
| C、α∥β,m?α,n?β,则m∥n |
| D、α∥γ,n?β,n?γ,α∩β=m,则m∥n |
考点:命题的真假判断与应用
专题:简易逻辑
分析:利用空间中线和面的位置关系,逐一核对四个选项即可得到正确的答案.
解答:
解:对于A,若m∥α,n∥α,可得m与n的位置关系有三种,即平行、相交和异面,A错误;
对于B,若α∥γ,n∥β,α∩β=m,如图,

此时n与m不平行,B错误;
对于C,若α∥β,m?α,n?β,可得m与n的位置关系有两种,即平行和异面,C错误;
对于D,若α∥γ,n?β,n?γ,α∩β=m,在上图中,
只是n限制为β与γ的交线,
∵α∥γ,
∴由两面平行的性质定理可得m∥n,D正确.
故选:D.
对于B,若α∥γ,n∥β,α∩β=m,如图,

此时n与m不平行,B错误;
对于C,若α∥β,m?α,n?β,可得m与n的位置关系有两种,即平行和异面,C错误;
对于D,若α∥γ,n?β,n?γ,α∩β=m,在上图中,
只是n限制为β与γ的交线,
∵α∥γ,
∴由两面平行的性质定理可得m∥n,D正确.
故选:D.
点评:本题考查命题的真假判断与应用,考查了空间中的线和面的位置关系,考查了学生的空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
 已知函数f(x)=2sin(2x+φ)(x∈R)的图象的一部分如图所示,将函数f(x)的图象向左平移α(α>0)个单位后得到的图象关于y轴对称,则α的最小值为( )
已知函数f(x)=2sin(2x+φ)(x∈R)的图象的一部分如图所示,将函数f(x)的图象向左平移α(α>0)个单位后得到的图象关于y轴对称,则α的最小值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为
,D为BC中点,则三棱锥A-B1DC1的体积为( )
| 3 |
| A、3 | ||||
B、
| ||||
| C、1 | ||||
D、
|
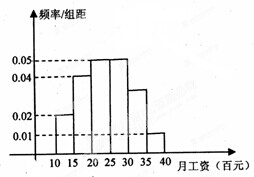 为了解工薪阶层的收入情况,某地政府调查了1000人的月工资收入,并把调查结果画成如图所示的频率分布直方图,则由图知月工资在(30,35](百元)的人数为( )
为了解工薪阶层的收入情况,某地政府调查了1000人的月工资收入,并把调查结果画成如图所示的频率分布直方图,则由图知月工资在(30,35](百元)的人数为( )| A、80 | B、150 |
| C、230 | D、400 |
 如图,三棱柱ABC-A1B1C1中,AA1⊥BC,A1B⊥BB1,
如图,三棱柱ABC-A1B1C1中,AA1⊥BC,A1B⊥BB1,