题目内容
18.设奇函数f(x)在(0,+∞)上为增函数,且$f({\sqrt{3}})=0$,则不等式x[f(x)-f(-x)]<0的解集为( )| A. | $({-\sqrt{3},0})∪({\sqrt{3},+∞})$ | B. | $({-\sqrt{3},0})∪({0,\sqrt{3}})$ | C. | $({-∞,-\sqrt{3}})∪({0,\sqrt{3}})$ | D. | $({-∞,-\sqrt{3}})∪({\sqrt{3},+∞})$ |
分析 根据条件可以得到f(x)在(-∞,0)上为增函数,且$f(-\sqrt{3})=0$,f(x)为奇函数,便有f(-x)=-f(x),从而不等式x[f(x)-f(-x)]<0可变成xf(x)<0,从而可得到$\left\{\begin{array}{l}{x>0}\\{f(x)<f(\sqrt{3})}\end{array}\right.$,或$\left\{\begin{array}{l}{x<0}\\{f(x)>f(-\sqrt{3})}\end{array}\right.$,根据f(x)的单调性便可解出这两个不等式组,从而便求出原不等式的解集.
解答 解:f(x)为奇函数,在(0,+∞)上为增函数;
∴f(x)在(-∞,0)上为增函数;
∵f($\sqrt{3}$)=0,∴$f(-\sqrt{3})=0$;
由x[f(x)-f(-x)]<0得,2xf(x)<0;
∴xf(x)<0;
∴$\left\{\begin{array}{l}{x>0}\\{f(x)<0}\end{array}\right.$,或$\left\{\begin{array}{l}{x<0}\\{f(x)>0}\end{array}\right.$;
即$\left\{\begin{array}{l}{x>0}\\{f(x)<f(\sqrt{3})}\end{array}\right.$,或$\left\{\begin{array}{l}{x<0}\\{f(x)>f(-\sqrt{3})}\end{array}\right.$;
根据f(x)的单调性解得$0<x<\sqrt{3}$,或$-\sqrt{3}<x<0$;
∴原不等式的解集为$(-\sqrt{3},0)∪(0,\sqrt{3})$.
故选:B.
点评 考查奇函数的定义,奇函数在对称区间上的单调性特点,两个因式乘积的不等式转化成不等式组求解的方法,根据增函数的定义解不等式的方法.

| A. | $80\sqrt{5}$ | B. | $60\sqrt{5}$ | C. | $40\sqrt{5}$ | D. | $20\sqrt{5}$ |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
| A. | 已知命题p和q,若“p∨q”为假命题,则命题p和q中必一真一假 | |
| B. | 命题“?c∈R,方程2x2+y2=c表示椭圆”的否定是“?c∈R,方程2x2+y2=c不表示椭圆” | |
| C. | 命题“若k<9,则方程“$\frac{x^2}{25-k}$+$\frac{y^2}{k-9}$=1表示双曲线”是假命题 | |
| D. | 命题“在△ABC中,若sinA<$\frac{1}{2}$,则A<$\frac{π}{6}$”的逆否命题为真命题 |
| A. | a2>b2 | B. | |a|>|b| | C. | lg(a-b)>0 | D. | ($\frac{1}{2}$)a>($\frac{1}{2}$)b |
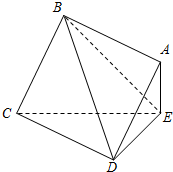 如图,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,
如图,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,