题目内容
7.设a,b∈R,且a<b,则下列等式成立的是( )| A. | a2>b2 | B. | |a|>|b| | C. | lg(a-b)>0 | D. | ($\frac{1}{2}$)a>($\frac{1}{2}$)b |
分析 根据a,b的符号举出反例判断.
解答 解:当0<a<b时,有a2<b2,|a|<|b|,故A,B错误;
当a<b时,a-b<0,故lg(a-b)无意义,故C错误;
∵y=($\frac{1}{2}$)x在R上是减函数,∴($\frac{1}{2}$)a>($\frac{1}{2}$)b,故D正确.
故选:D.
点评 本题考查了基本不等式的性质,举出反例是判断关键.

练习册系列答案
相关题目
18.设奇函数f(x)在(0,+∞)上为增函数,且$f({\sqrt{3}})=0$,则不等式x[f(x)-f(-x)]<0的解集为( )
| A. | $({-\sqrt{3},0})∪({\sqrt{3},+∞})$ | B. | $({-\sqrt{3},0})∪({0,\sqrt{3}})$ | C. | $({-∞,-\sqrt{3}})∪({0,\sqrt{3}})$ | D. | $({-∞,-\sqrt{3}})∪({\sqrt{3},+∞})$ |
12.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)虚轴上的端点B(0,b),右焦点F,若以B为圆心的圆与C的一条渐近线相切于点P,且$\overrightarrow{BP}$$∥\overrightarrow{PF}$,则该双曲线的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\frac{1+\sqrt{3}}{2}$ | D. | $\frac{1+\sqrt{5}}{2}$ |
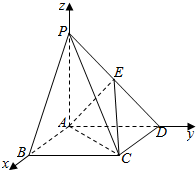 已知正方形ABCD的边长为2,PA⊥平面ABCD,且PA=2,E是PD中点.以A为原点,建立如图所示的空间直角坐标系A-xyz.
已知正方形ABCD的边长为2,PA⊥平面ABCD,且PA=2,E是PD中点.以A为原点,建立如图所示的空间直角坐标系A-xyz.