题目内容
6.已知平面内三点A,B,C满足|$\overrightarrow{AB}$|=|$\overrightarrow{CA}$|=1,|$\overrightarrow{BC}$|=$\sqrt{3}$,则$\overrightarrow{AB}$•$\overrightarrow{BC}$为( )| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
分析 由余弦定理可得:cosB,再利用数量积运算性质可得:$\overrightarrow{AB}$•$\overrightarrow{BC}$.
解答 解:由余弦定理可得:cosB=$\frac{{1}^{2}+(\sqrt{3})^{2}-{1}^{2}}{2×1×\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,
∴$\overrightarrow{AB}$•$\overrightarrow{BC}$=-1×$\sqrt{3}$cosB=-$\frac{3}{2}$.
故选B
点评 本题考查了余弦定理、向量数量积运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.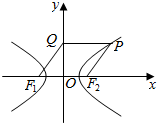 已知点P在以F1,F2为焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,过P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该双曲线的离心率为( )
已知点P在以F1,F2为焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,过P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该双曲线的离心率为( )
 已知点P在以F1,F2为焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,过P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该双曲线的离心率为( )
已知点P在以F1,F2为焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,过P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该双曲线的离心率为( )| A. | $\frac{1+\sqrt{2}}{2}$ | B. | $\frac{1+\sqrt{3}}{2}$ | C. | 1$+\sqrt{2}$ | D. | 1+$\sqrt{3}$ |
1.已知点A(0,0,0),B(1,0,1),C(0,1,1),则平面ABC的一个法向量$\overrightarrow m$是( )
| A. | (1,1,1) | B. | (1,1,-1) | C. | (-1,1,1) | D. | (1,-1,1) |
18.设奇函数f(x)在(0,+∞)上为增函数,且$f({\sqrt{3}})=0$,则不等式x[f(x)-f(-x)]<0的解集为( )
| A. | $({-\sqrt{3},0})∪({\sqrt{3},+∞})$ | B. | $({-\sqrt{3},0})∪({0,\sqrt{3}})$ | C. | $({-∞,-\sqrt{3}})∪({0,\sqrt{3}})$ | D. | $({-∞,-\sqrt{3}})∪({\sqrt{3},+∞})$ |
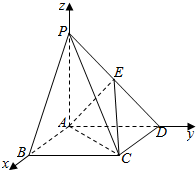 已知正方形ABCD的边长为2,PA⊥平面ABCD,且PA=2,E是PD中点.以A为原点,建立如图所示的空间直角坐标系A-xyz.
已知正方形ABCD的边长为2,PA⊥平面ABCD,且PA=2,E是PD中点.以A为原点,建立如图所示的空间直角坐标系A-xyz.