题目内容
在等比数列{an}中，己知a1=2，a4=16．
（1）求数列{an}的通项公式；
（2）若a3，a5分别为等差数列{bn}的第3项和第5项，试求数列{bn}的通项公式及数列{anbn}前n项和Sn．
（1）求数列{an}的通项公式；
（2）若a3，a5分别为等差数列{bn}的第3项和第5项，试求数列{bn}的通项公式及数列{anbn}前n项和Sn．
考点：等比数列的性质,数列的求和
专题：计算题,等差数列与等比数列
分析：（1）根据等比数列{an}中，a1=2，a4=16，求出公比，即可求出数列{an}的通项公式；
（2）利用a3，a5分别为等差数列{bn}的第3项和第5项，求出数列{bn}的首项与公差，即可确定通项公式，利用错位相减法，可求数列{anbn}前n项和Sn．
（2）利用a3，a5分别为等差数列{bn}的第3项和第5项，求出数列{bn}的首项与公差，即可确定通项公式，利用错位相减法，可求数列{anbn}前n项和Sn．
解答：
解：（1）∵等比数列{an}中，a1=2，a4=16，
∴q=2，
∴an=2•2n-1=2n；
（2）∵a3，a5分别为等差数列{bn}的第3项和第5项，
∴
，
∴
，
∴bn=-16+12（n-1）=12n-28，
∴anbn=（12n-28）•2n，
∴Sn=-16•2+（-4）•22+…+（12n-28）•2n，
∴2Sn=-16•22+…+（12n-40）•2n+（12n-28）•2n+1，
两式相减可得-Sn=-16•2+12•22+…+12•2n-（12n-28）•2n+1=12•
-56-（12n-28）•2n+1，
∴Sn=（3n-10）•2n+3-80．
∴q=2，
∴an=2•2n-1=2n；
（2）∵a3，a5分别为等差数列{bn}的第3项和第5项，
∴
|
∴
|
∴bn=-16+12（n-1）=12n-28，
∴anbn=（12n-28）•2n，
∴Sn=-16•2+（-4）•22+…+（12n-28）•2n，
∴2Sn=-16•22+…+（12n-40）•2n+（12n-28）•2n+1，
两式相减可得-Sn=-16•2+12•22+…+12•2n-（12n-28）•2n+1=12•
| 2(1-2n) |
| 1-2 |
∴Sn=（3n-10）•2n+3-80．
点评：本题考查等差数列与等比数列的通项，考查数列的求和，考查错位相减法，考查学生的计算能力，属于中档题．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
已知三条不重合的直线m，n，l和两个不重合的平面α、β，下列命题中正确命题个数为（ ）
①若m∥n，n?α，则m∥α；②若l⊥α，m⊥β且l⊥m则α⊥β
③若l⊥n，m⊥n，则l∥m④若α⊥β，α∩β=m，n?β，n⊥m，则n⊥α
①若m∥n，n?α，则m∥α；②若l⊥α，m⊥β且l⊥m则α⊥β
③若l⊥n，m⊥n，则l∥m④若α⊥β，α∩β=m，n?β，n⊥m，则n⊥α
| A、1 | B、2 | C、3 | D、4 |
已知集合A={x||2x+1|＞3}，集合B={x|y=
}，则A∩（∁RB）=（ ）
|
| A、（1，2） |
| B、（1，2] |
| C、（1，+∞） |
| D、[1，2] |
某商家推出一款简单电子游戏，弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上（如图），用S表示这三个球为顶点的三角形的面积．规定：当三球共线时，S=0；当S最大时，中一等奖，当S最小时，中二等奖，其余情况不中奖，一次游戏只能弹射一次．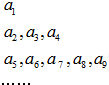
将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表，已知图中的第一列数a1，a2，a5…构成一个等差数列，记为数列{bn}，且b2=4，b5=10，图中每一行正中间一个数a1，a3，a7…构成数列{cn}，其前n项和为Sn．