题目内容
若函数f(x)对定义域中任意x,均满足f(x)+f(2a-x)=2b,则称函数y=f(x)的图象关于点(a,b)对称,
(1)已知函数g(x)在(-∞,0)∪(0,+∞)上的图象关于点(0,1)对称,且当x∈(0,+∞)时,g(x)=x2+ax+1,求函数g(x)在x∈(-∞,0)上的解析式;
(2)已知函数f(x)=
的图象关于点(0,1)对称,在(1)的条件下,若对实数x<0及t>0,恒有g(x)<f(t),求实数a的取值范围.
(1)已知函数g(x)在(-∞,0)∪(0,+∞)上的图象关于点(0,1)对称,且当x∈(0,+∞)时,g(x)=x2+ax+1,求函数g(x)在x∈(-∞,0)上的解析式;
(2)已知函数f(x)=
| x2+mx+m |
| x |
考点:函数恒成立问题
专题:函数的性质及应用
分析:(1)利用函数g(x)在(-∞,0)∪(0,+∞)上的图象关于点(0,1)对称,可得g(x)+g(-x)=2,根据x∈(0,+∞)时的解析式,即可求得结论;
(2)对任意实数x∈(-∞,0),恒有g(x)<f(t)成立,等价于g(x)max<f(t)min,由此可求实数a的取值范围.
(2)对任意实数x∈(-∞,0),恒有g(x)<f(t)成立,等价于g(x)max<f(t)min,由此可求实数a的取值范围.
解答:
解:(1)∵函数g(x)在(-∞,0)∪(0,+∞)上的图象关于点(0,1)对称,
∴g(x)+g(-x)=2,
∵当x∈(0,+∞)时,g(x)=x2+ax+1,
∴当x<0时,g(x)=2-g(-x)=-x2+ax+1,
即g(x)=-x2+ax+1,x<0;
(2)由题设,∵函数f(x)=
的图象关于点(0,1)对称,
∴f(x)+f(-x)=2,
∴
+
=2
∴m=1,
∵f(t)=
=t+
+m=t+
+1≥2
+1=3,其最小值为f(1)=3,
g(x)=-x2+ax+1=-(x-
)2+
+1,
①当
<0,即a<0时,g(x)max=
+1<3,即a2<8,解得-2
<a<0,
②当
≥0,即a≥0时,g(x)max<1<3,
∴a∈[0,+∞),
由①、②得a>-2
,
故实数a的取值范围是a>-2
.
∴g(x)+g(-x)=2,
∵当x∈(0,+∞)时,g(x)=x2+ax+1,
∴当x<0时,g(x)=2-g(-x)=-x2+ax+1,
即g(x)=-x2+ax+1,x<0;
(2)由题设,∵函数f(x)=
| x2+mx+m |
| x |
∴f(x)+f(-x)=2,
∴
| x2+mx+m |
| x |
| x2-mx+m |
| -x |
∴m=1,
∵f(t)=
| t2+tm+m |
| t |
| m |
| t |
| 1 |
| t |
t•
|
g(x)=-x2+ax+1=-(x-
| a |
| 2 |
| a2 |
| 4 |
①当
| a |
| 2 |
| a2 |
| 4 |
| 2 |
②当
| a |
| 2 |
∴a∈[0,+∞),
由①、②得a>-2
| 2 |
故实数a的取值范围是a>-2
| 2 |
点评:本题主要考查函数的对称性,考查函数的解析式,考查恒成立问题,正确求出函数的最值是关键.综合性较强,运算量较大.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
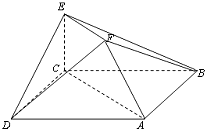 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=| 2 |
(1)求证:平面BEF⊥平面DEF;
(2)求二面角A-BF-E的余弦值.
关于函数f(x)=2-x+lnx,下列说法正确的是( )
| A、无零点 |
| B、有且仅有一个零点 |
| C、有两个零点x1,x2,且(x1-1)(x2-1)>0 |
| D、有两个零点x1,x2,且(x1-1)(x2-1)<0 |