题目内容
8.已知函数f(x)=log3x+x+m在区间($\frac{1}{3}$,9)上有零点,则实数m的取值范围是-11<m<$\frac{2}{3}$.分析 根据零点的性质,f($\frac{1}{3}$)f(9)<0,即可求出实数m的取值范围.
解答 解:∵y1=x单调递增,y2=log3x单调递增
∴f(x)=log3x+x+m单调递增
又∵数f(x)=log3x+x+m在区间($\frac{1}{3}$,9)上有零点,
∴f($\frac{1}{3}$)f(9)<0,
∴(-1+$\frac{1}{3}$+m)(2+9+m)<0,
∴-11<m<$\frac{2}{3}$.
故答案为:-11<m<$\frac{2}{3}$.
点评 本题考查函数的零点,要求熟练掌握零点的性质.属简单题

练习册系列答案
相关题目
16.定义A*B、B*C、C*D、D*B分别对应下列图形,
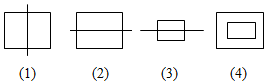
那么下面的图形中,可以表示A*D,A*C的分别是( )
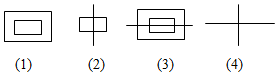

那么下面的图形中,可以表示A*D,A*C的分别是( )

| A. | (1)、(2) | B. | (2)、(3) | C. | (2)、(4) | D. | (1)、(4) |
17.设a=20.4,b=30.75,c=log3$\frac{1}{3}$,则( )
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | b>c>a |
18.在正方体ABCD-A1B1C1D1中,E,F分别为棱AB,BB1的中点,则直线BC1与EF所成角的余弦值是( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
 为了解某地脐橙种植情况,调研小组在该地某脐橙种植园中随机抽出30棵,每棵挂果情况编成如图所示的茎叶图(单位:个):若挂果在175个以上(包括175)定义为“高产”,挂果在175个以下(不包括175)定义为“非高产”.
为了解某地脐橙种植情况,调研小组在该地某脐橙种植园中随机抽出30棵,每棵挂果情况编成如图所示的茎叶图(单位:个):若挂果在175个以上(包括175)定义为“高产”,挂果在175个以下(不包括175)定义为“非高产”.