题目内容
9．设f（x）=f′（1）+$\sqrt{x}$．则f（4）=$\frac{5}{2}$．分析 先求出f（x）的导数，得到f′（1）的值，求出f（x）的表达式，从而求出f（4）的值即可．
解答 解：∵f（x）=f′（1）+$\sqrt{x}$，
∴f′（x）=$\frac{1}{2\sqrt{x}}$，
∴f′（1）=$\frac{1}{2}$，
∴f（4）=$\frac{1}{2}$+$\sqrt{4}$=$\frac{5}{2}$，
故答案为：$\frac{5}{2}$．
点评 本题考查了导数的运算问题，考查求函数的表达式，是一道基础题．
练习册系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
19．下列四个函数①y=x3；②y=x2+1；③y=|x|；④y=2x在x=0处取得极小值的函数是（ ）
| A． | ①② | B． | ②③ | C． | ③④ | D． | ①③ |
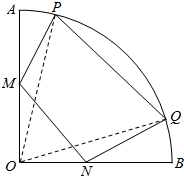如图，在半径为2，圆心角为$\frac{π}{2}$的扇形金属材料中剪出一个四边形MNQP，其中M、N两点分別在半径OA、OB上，P、Q两点在弧$\widehat{AB}$上，且OM=ON，MN∥PQ．