题目内容
19.在一个港口,相邻两次高潮发生时间相距12h,低潮时水的深度为8.4m,高潮时为16m.一次高潮发生在10月10日4:00.每天涨潮落潮时,水的深度d(m)与时间t(h)近似满足关系式d=Asin(ωt+φ)+h.(1)若从10月10日0:00开始计算,求该港口的水深d(m)和时间t(h)之间的函数关系;
(2)10月10日17:00该港口水深约为多少?(精确到0.1m)
(3)10月10日这一天该港口共有多少时间水深低于10.3m?
分析 (1)设d=Asin(ωt+φ)+h,利用低潮时入口处水的深度为8.4m,高潮时为16m,求出h,A,利用两次高潮发生的时间间隔12h,求出ω,再求出φ,即可描述这个港口的水深d(m)和时间t(h)之间的函数关系;
(2)10月10日17:00,t=17,即可求出水的深度;
(3)d=3.8sin($\frac{π}{6}$t-$\frac{π}{6}$)+12.2≤10.3,即可求出10月10日这一天该港口共有多少时间水深低于10.3m.
解答 解:(1)由题意,$\left\{\begin{array}{l}{A+h=16}\\{-A+h=8.4}\end{array}\right.$,∴h=12.2,A=3.8,
∵T=12,
∴ω=$\frac{π}{6}$,
t=4时,4ω+φ=$\frac{π}{2}$,∴φ=-$\frac{π}{6}$,
∴d=3.8sin($\frac{π}{6}$t-$\frac{π}{6}$)+12.2;
(2)t=17时,d=3.8sin($\frac{π}{6}$×17-$\frac{π}{6}$)+12.2≈15.5;
(3)d=3.8sin($\frac{π}{6}$t-$\frac{π}{6}$)+12.2<10.3,
∴$\frac{7}{6}$π<$\frac{π}{6}$t-$\frac{π}{6}$<$\frac{11}{6}$π,
∴8<t<12,
∴10月10日这一天该港口共有10h水深低于10.3m.
点评 本题考查在实际问题中建立三角函数模型,考查学生利用数学知识解决实际问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知x0是函数f(x)=-2x+$\frac{3}{x}$的一个零点.若x1∈(1,x0),x2∈(x0,+∞),则( )
| A. | f(x1)<0,f(x2)<0 | B. | f(x1)<0,f(x2)>0 | C. | f(x1)>0,f(x2)>0 | D. | f(x1)>0,f(x2)<0 |
4.圆台的上下底面半径分别为1和2,它的侧面展开图对应扇形的圆心角为180°,那么圆台的表面积是( )
| A. | 5π | B. | 7π | C. | 9π | D. | 11π |
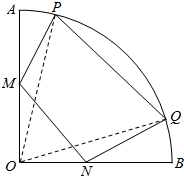 如图,在半径为2,圆心角为$\frac{π}{2}$的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧$\widehat{AB}$上,且OM=ON,MN∥PQ.
如图,在半径为2,圆心角为$\frac{π}{2}$的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧$\widehat{AB}$上,且OM=ON,MN∥PQ.