题目内容
2.已知平面向量$\overrightarrow a$和$\overrightarrow b$的夹角等于$\frac{π}{3}$,$|{\overrightarrow a}|=2$,$|{\overrightarrow b}|=1$,则$|{\overrightarrow a-2\overrightarrow b}|$=( )| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
分析 计算($\overrightarrow{a}-2\overrightarrow{b}$)2,再开方得出$|{\overrightarrow a-2\overrightarrow b}|$.
解答 解:$\overrightarrow{a}•\overrightarrow{b}$=2×$1×cos\frac{π}{3}$=1,
∴($\overrightarrow{a}-2\overrightarrow{b}$)2=${\overrightarrow{a}}^{2}$+4${\overrightarrow{b}}^{2}$-4$\overrightarrow{a}•\overrightarrow{b}$=4,
∴$|{\overrightarrow a-2\overrightarrow b}|$=2.
故选A.
点评 本题考查了平面向量的模长计算,数量积运算,属于中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
12.5张奖券中只有1张能中奖,现分别由5名同学无放回地抽取,若已知第一名同学没有抽到中奖券,则最后一名同学抽到中奖奖券的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
13.已知f(x)为R上的可导函数,且?x∈R,均有f(x)+f'(x)<0,则以下判断正确的是( )
| A. | e2017•f(2017)>f(0) | B. | e2017•f(2017)=f(0) | ||
| C. | e2017•f(2017)<f(0) | D. | e2017f(2017)与f(0)的大小无法确定 |
11.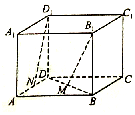 如图所示,在正方体ABCD-A1B1C1D1中,已知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
如图所示,在正方体ABCD-A1B1C1D1中,已知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
 如图所示,在正方体ABCD-A1B1C1D1中,已知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
如图所示,在正方体ABCD-A1B1C1D1中,已知棱长为a,M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )| A. | $\frac{\sqrt{30}}{10}$ | B. | $\frac{\sqrt{30}}{10}$a | C. | -$\frac{\sqrt{30}}{10}$ | D. | $\frac{\sqrt{15}}{15}$a |
15.单位正方体(棱长为1)被切去一部分,剩下部分几何体的三视图如图所示,则( )


| A. | 该几何体体积为$\frac{5}{6}$ | B. | 该几何体体积可能为$\frac{2}{3}$ | ||
| C. | 该几何体表面积应为$\frac{9}{2}+\frac{{\sqrt{3}}}{2}$ | D. | 该几何体表面积应为$\frac{7}{2}+\frac{{\sqrt{3}}}{2}$ |