题目内容
函数f（x）=
的定义域为（ ）
| lg(2-x) | ||
|
| A、（-3，2） |
| B、[-3，2） |
| C、（-∞，-3） |
| D、（-∞，-3] |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件，建立不等式关系即可求出函数的定义域．
解答：
解：要使函数f（x）有意义，则
，
即
，则
，
解得-3＜x＜2，
故函数的定义域为（-3，2），
故选：B．
|
即
|
|
解得-3＜x＜2，
故函数的定义域为（-3，2），
故选：B．
点评：本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件．
练习册系列答案
相关题目
已知α是第四象限的角，并且cosα=
，那么tanα的值等于（ ）
| 4 |
| 5 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
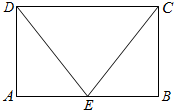如图，矩形ABCD中，点E为边AB的中点，若在矩形ABCD内部随机取一个点Q，则点Q取自△AED或△BEC内部的概率等于（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
设函数y=sinx的定义域为[a，b]，值域为[-
，1]，给出以下四个结论：
①b-a的最小值为
②b-a的最大值为
③a可能等于2kπ-
（k∈z）
④b可能等于2kπ-
（k∈z）
其中正确的有（ ）
| 1 |
| 2 |
①b-a的最小值为
| 2π |
| 3 |
②b-a的最大值为
| 4π |
| 3 |
③a可能等于2kπ-
| π |
| 6 |
④b可能等于2kπ-
| π |
| 6 |
其中正确的有（ ）
| A、4个 | B、3个 | C、2个 | D、1个 |
A={x|y=
}，B={y|y=
}，则A∪B=（ ）
| 2x-x2 |
| x2+1 |
| x2 |
| A、（1，2] |
| B、[0，1）∪（1，2] |
| C、[0，+∞] |
| D、[0，2] |
两个焦点的坐标分别为（-3，0），（3，0）的椭圆上的任一点到两焦点的距离之和为8，则椭圆的标准方程
为（ ）
为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列图形中，哪个是函数y=|-x2+2x|的简图（ ）
A、 |
B、 |
C、 |
D、 |
双曲线的两焦点坐标是F1（3，0），F2（-3，0），2b=4，则双曲线的标准方程是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|