题目内容
下列命题中,正确的命题个数是 .
①a>b⇒ac2>bc2;
②a≥b⇒ac2≥bc2;
③
>
⇒ac>bc,
④
≥
⇒ac≥bc,
⑤
⇒c>0;
⑥
⇒c≥0.
①a>b⇒ac2>bc2;
②a≥b⇒ac2≥bc2;
③
| a |
| c |
| b |
| c |
④
| a |
| c |
| b |
| c |
⑤
|
⑥
|
考点:不等式的基本性质
专题:作差法,推理和证明
分析:1.从条件或结论入手,采用作差比较法;
2.取特殊值验证,找出假命题.
3.分类讨论法
2.取特殊值验证,找出假命题.
3.分类讨论法
解答:
解:对①:当a>b,c=0时,有ac2=bc2,①为假命题.
对②:当c=0时,由a≥b,得ac2=bc2,即ac2≥bc2成立;
当c≠0时,则c2>0,由a≥b,得ac2≥bc2,②为真命题.
对③:由
>
知,c≠0,则c2>0,所以
•c2>
•c2,即ac>bc,③为真命题.
对④:
≥
⇒
≥0,
当c>0时,有a-b≥0,即a≥b,所以ac≥bc;
当c<0时,有a-b≤0,即a≤b,所以ac≥bc,故④为真命题.
对⑤:由ac>bc⇒(a-b)c>0,又a>b,
∴c>0,故⑤为真命题.
对⑥:取a=b=1,c=-2,满足
,但c≥0不成立,故⑥为假命题.
∴正确的命题个数是4,故答案为4.
对②:当c=0时,由a≥b,得ac2=bc2,即ac2≥bc2成立;
当c≠0时,则c2>0,由a≥b,得ac2≥bc2,②为真命题.
对③:由
| a |
| c |
| b |
| c |
| a |
| c |
| b |
| c |
对④:
| a |
| c |
| b |
| c |
| a-b |
| c |
当c>0时,有a-b≥0,即a≥b,所以ac≥bc;
当c<0时,有a-b≤0,即a≤b,所以ac≥bc,故④为真命题.
对⑤:由ac>bc⇒(a-b)c>0,又a>b,
∴c>0,故⑤为真命题.
对⑥:取a=b=1,c=-2,满足
|
∴正确的命题个数是4,故答案为4.
点评:1.本题考查了不等式的基本性质,作差比较法,分析法与综合法,容易出错,要求对问题考虑周全,有谨密的思维能力才能正确作出判断.
2.要说明一个命题为真命题,必须有严密的逻辑推理;要说明一个命题为假命题,只需举出一个反例即可.
2.要说明一个命题为真命题,必须有严密的逻辑推理;要说明一个命题为假命题,只需举出一个反例即可.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
如图的程序输出的结果是( )


| A、3 | B、5 | C、9 | D、13 |

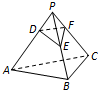 如图,正三棱锥P-ABC的所有棱长都为4.点D,E,F分别在棱PA,PB,PC上,满足DE=EF=3,DF=2的△DEF个数是( )
如图,正三棱锥P-ABC的所有棱长都为4.点D,E,F分别在棱PA,PB,PC上,满足DE=EF=3,DF=2的△DEF个数是( )