题目内容
1.已知连续不断函数f(x)=sinx+x-$\frac{π}{4}$(0<x<$\frac{π}{2}$),g(x)=cosx-x+$\frac{π}{4}$(0<x<$\frac{π}{2}$).(1)求证:函数f(x)在区间(0,$\frac{π}{2}$)上有且只有一个零点;
(2)现已知函数g(x)在(0,$\frac{π}{2}$)上有且只有一个零点(不必证明),记f(x)和g(x)在(0,$\frac{π}{2}$)上的零点分别为x1,x2,求证:x1+x2=$\frac{π}{2}$.
分析 (1)可判断f(0)=-$\frac{π}{4}$<0,f($\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$>0,再判断函数的单调性,从而证明.
(2)化简可得cos($\frac{π}{2}$-x1)-($\frac{π}{2}$-x1)+$\frac{π}{4}$=0,从而证明.
解答 证明:(1)∵f(0)=-$\frac{π}{4}$<0,f($\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$>0,
∴f(x)在区间(0,$\frac{π}{2}$)上有一个零点;
又∵f(x)=sinx+x-$\frac{π}{4}$在(0,$\frac{π}{2}$)上单调递增,
∴f(x)在(0,$\frac{π}{2}$)上有且只有一个零点;
(2)∵f(x)在区间(0,$\frac{π}{2}$)上有且只有一个零点x1,
∴f(x1)=sinx1+x1-$\frac{π}{4}$=0,
即cos($\frac{π}{2}$-x1)-($\frac{π}{2}$-x1)+$\frac{π}{4}$=0,
又∵函数g(x)在(0,$\frac{π}{2}$)上有且只有一个零点x2,
∴$\frac{π}{2}$-x1=x2,
即x1+x2=$\frac{π}{2}$.
点评 本题考查了函数的零点的判定定理的应用及函数的性质的判断与应用.

练习册系列答案
相关题目
1.在△ABC中,若tanA=$\frac{1}{3}$,tanB=-2,则角C等于( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
9.设偶函数f(x)满足f(x)=2x-4(x≥0),则{x|f(x-2)<0}=( )
| A. | {x|x<-2或x>4} | B. | {x|x<0或x>4} | C. | {x|x<0或x>6} | D. | {x|0<x<4} |
16.若f(x)=x2+2x-3,则f(x)在区间[-2,1]上的值域是( )
| A. | [-4,-3] | B. | [-3,0] | C. | [-4,0] | D. | [0,2] |
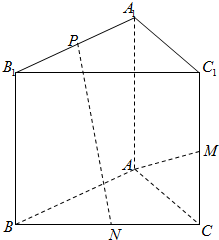 已知如图,在直三棱柱ABC-A1B1C1中,AA1=AC,且AB⊥AC,M是面CC1的中点,N是BC的中点,点P在直线A1B1上.
已知如图,在直三棱柱ABC-A1B1C1中,AA1=AC,且AB⊥AC,M是面CC1的中点,N是BC的中点,点P在直线A1B1上.