题目内容
13.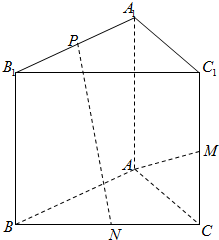 已知如图,在直三棱柱ABC-A1B1C1中,AA1=AC,且AB⊥AC,M是面CC1的中点,N是BC的中点,点P在直线A1B1上.
已知如图,在直三棱柱ABC-A1B1C1中,AA1=AC,且AB⊥AC,M是面CC1的中点,N是BC的中点,点P在直线A1B1上.(Ⅰ)若P为A1B1中点,求证:NP∥平面ACC1A1;
(Ⅱ)证明:PN⊥AM.
分析 (Ⅰ)以A为原点,AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能求出NP∥平面ACC1A1.
(2)求出$\overrightarrow{AM}$=(0,2,1),$\overrightarrow{PN}$=(0,1,-2),利用向量法能证明PN⊥AM.
解答  证明:(Ⅰ)以A为原点,AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,
证明:(Ⅰ)以A为原点,AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,
设AA1=AC=2,AB=2a,
则B(2a,0,0),C(0,2,0),N(a,1,0),P(a,0,2),
$\overrightarrow{NP}$=(0,-1,2),平面ACC1A1的法向量$\overrightarrow{n}$=(1,0,0),
$\overrightarrow{NP}•\overrightarrow{n}$=0,
∵NP?平面ACC1A1,∴NP∥平面ACC1A1.
(2)M(0,2,1),$\overrightarrow{AM}$=(0,2,1),
又$\overrightarrow{PN}$=(0,1,-2),
∴$\overrightarrow{PN}•\overrightarrow{AM}$=0+2-2=0,
∴$\overrightarrow{PN}$⊥$\overrightarrow{AM}$,
∴PN⊥AM.
点评 本题考查直线与平面平行的证明,考查直线与平面垂直的证明,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
12.若函数f(x)=x2+bx+4恰有一个零点,则b=( )
| A. | 4 | B. | 16 | C. | -4 | D. | ±4 |
5.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与直线y=m(0<m<A)的三个相邻交点的横坐标分别为3,5,11,则f(x)的单调递减区间是( )
| A. | [8k,8k+4],k∈Z | B. | [8kπ,8kπ+4],k∈Z | C. | [8k-4,8k],k∈Z | D. | [8kπ-4,8kπ],k∈Z |
3.设f(x)=$\left\{\begin{array}{l}{2{e}^{x-1}(x<2)}\\{\frac{1}{2}+lnx(x≥2)}\end{array}\right.$,则f(f(e))的值为( )
| A. | 0 | B. | $\sqrt{e}$ | C. | 2$\sqrt{e}$ | D. | 3 |
 如图,ABCD-A1B1C1D1是正方体,E,F,G,H,M,N分别是所在棱的中点,则下列结论错误的有①③④
如图,ABCD-A1B1C1D1是正方体,E,F,G,H,M,N分别是所在棱的中点,则下列结论错误的有①③④