题目内容
给出下列四个命题:
①已知a,b,m都是正数,且
>
,则a<b;
②若函数f(x)=lg(ax+1)的定义域是{x|x<1},则a<-1;
③已知x∈(0,π),则y=sinx+
的最小值为2
;
④已知a、b、c成等比数列,a、x、b成等差数列,b、y、c也成等差数列,则
+
的值等于2;
⑤已知函数f(x)=ex-1,g(x)=-x2+4x-3,若有f(a)=g(b),则b的取值范围为(2-
,2+
).
其中正确命题的序号是 .
①已知a,b,m都是正数,且
| a+m |
| b+m |
| a |
| b |
②若函数f(x)=lg(ax+1)的定义域是{x|x<1},则a<-1;
③已知x∈(0,π),则y=sinx+
| 2 |
| sinx |
| 2 |
④已知a、b、c成等比数列,a、x、b成等差数列,b、y、c也成等差数列,则
| a |
| x |
| c |
| y |
⑤已知函数f(x)=ex-1,g(x)=-x2+4x-3,若有f(a)=g(b),则b的取值范围为(2-
| 2 |
| 2 |
其中正确命题的序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:①利用不等式的性质即可得出;
②取a=-2即可判断出;
③换元利用函数的单调性即可得出;
④先求出函数f(x)的值域,由f(a)=g(b),可知两个函数的值域相同,即可得出.
②取a=-2即可判断出;
③换元利用函数的单调性即可得出;
④先求出函数f(x)的值域,由f(a)=g(b),可知两个函数的值域相同,即可得出.
解答:
解:对于①,由且
>
,又a,b,m都是正数,∴b(a+m)-a(b+m)=m(b-a)>0,∴b-a>0,即a<b.故①正确;
对于②,令a=-2,此时函数f(x)=lg(-2x+1)的定义域是{x|x<
},不是{x|x<1},故②错误;
对于③,设sinx=t∈[0,1],则y=t+
,∵函数y=t+
在区间[0,1]上单调递减,
∴此函数的最小值是f(1)=3,即y=sinx+
的最小值为3,故③错误;
对于④,由题意,b2=ac,2x=a+b,2y=b+c,∴
+
=
+
=
=
=2,故④正确;
对于⑤,由题意,f(x)=ex-1>-1,
若有f(a)=g(b),则g(b)=-b2+4b-3>-1,解得2-
<b<2+
.故⑤正确.
综上可知:只有①④⑤正确.
故答案为:①④⑤.
| a+m |
| b+m |
| a |
| b |
对于②,令a=-2,此时函数f(x)=lg(-2x+1)的定义域是{x|x<
| 1 |
| 2 |
对于③,设sinx=t∈[0,1],则y=t+
| 2 |
| t |
| 2 |
| t |
∴此函数的最小值是f(1)=3,即y=sinx+
| 2 |
| sinx |
对于④,由题意,b2=ac,2x=a+b,2y=b+c,∴
| a |
| x |
| c |
| y |
| 2a |
| a+b |
| 2c |
| b+c |
| 4ac+2ab+2bc |
| ab+ac+b2+bc |
| 4ac+2ab+2bc |
| 2ac+ab+bc |
对于⑤,由题意,f(x)=ex-1>-1,
若有f(a)=g(b),则g(b)=-b2+4b-3>-1,解得2-
| 2 |
| 2 |
综上可知:只有①④⑤正确.
故答案为:①④⑤.
点评:本题考查了函数的单调性值域、一元二次不等式的解法等基础知识,属于基础题.

练习册系列答案
相关题目
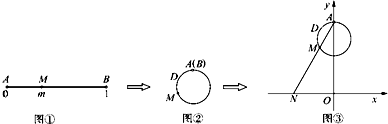 如图展示了一个由区间(0,1)到实数集R的映射过程:区间(0,1)中的实数m对应数轴上的点M,如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③.图③中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.
如图展示了一个由区间(0,1)到实数集R的映射过程:区间(0,1)中的实数m对应数轴上的点M,如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③.图③中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.