题目内容
给出如下四个命题:
①若“p且q”为假命题,则p、q均为假命题;
②命题p:“
≥0”则¬p:“
<0”
③对分类变量X与Y的随机变量K2的观测值k来说,k越小,判断“X与Y有关系”的把握越大;
④“x>0”是“x+
≥2”的充分必要条件.
其中正确的命题个数是( )
①若“p且q”为假命题,则p、q均为假命题;
②命题p:“
| x |
| x-1 |
| x |
| x-1 |
③对分类变量X与Y的随机变量K2的观测值k来说,k越小,判断“X与Y有关系”的把握越大;
④“x>0”是“x+
| 1 |
| x |
其中正确的命题个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:直接由复合命题的真值表判断①;写出命题的否定判断②;由分类变量X与Y的随机变量K2的观测值k的大小与“X与Y有关系”的把握程度判断③;由充分必要条件的概念判断④.
解答:
解:对于①,∵p,q中有一个为假命题,则“p且q”为假命题,
∴命题①错误;
对于②,命题p:“
≥0”则¬p:“
<0或x=1,”
∴命题②错误;
对于③,∵根据分类变量X与Y的随机变量K2的观测值k来说,k越小,“X与Y有关系”的可信程度越小,
∴命题③错误;
对于④,由x>0能得到x+
≥2,由x+
≥2能得到x>0,
∴“x>0”是“x+
≥2”的充分必要条件,
∴命题④正确.
∴正确命题的个数是1个.
故选:A.
∴命题①错误;
对于②,命题p:“
| x |
| x-1 |
| x |
| x-1 |
∴命题②错误;
对于③,∵根据分类变量X与Y的随机变量K2的观测值k来说,k越小,“X与Y有关系”的可信程度越小,
∴命题③错误;
对于④,由x>0能得到x+
| 1 |
| x |
| 1 |
| x |
∴“x>0”是“x+
| 1 |
| x |
∴命题④正确.
∴正确命题的个数是1个.
故选:A.
点评:本题考查命题的真假判断与运用,考查复合命题的真假判断,解答此题的关键在于对教材基础知识的掌握,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
对于直线m、n和平面α、β、γ,有如下五个命题:
①若m∥α,m⊥n,则n⊥α;
②若m⊥α,m⊥n,则n∥α;
③若α⊥β,γ⊥β,则α∥γ;
④若m⊥α,m∥n,n?β,则α⊥β;
⑤若α∩β=m,β∩γ=n,m∥n,则α∥γ;
其中正确的命题个数为( )
①若m∥α,m⊥n,则n⊥α;
②若m⊥α,m⊥n,则n∥α;
③若α⊥β,γ⊥β,则α∥γ;
④若m⊥α,m∥n,n?β,则α⊥β;
⑤若α∩β=m,β∩γ=n,m∥n,则α∥γ;
其中正确的命题个数为( )
| A、0个 | B、1个 | C、2个 | D、3个 |
 函数f(x)=x2(0<x<1)的图象如图所示,其在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交与点P、Q,点N(1,0),若△PQN的面积为S时点M恰好有两个,则S的取值范围为( )
函数f(x)=x2(0<x<1)的图象如图所示,其在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交与点P、Q,点N(1,0),若△PQN的面积为S时点M恰好有两个,则S的取值范围为( )A、[
| ||||
B、(
| ||||
C、(
| ||||
D、[
|
下列四个命题中,不正确的命题是( )
| A、如果一条直线与两条平行直线中的一条垂直,那么也和另一条垂直 |
| B、已知直线a、b、c,a∥b,c与a、b都不相交,若c与a所成的角为θ,则c与b所成的角也等于θ |
| C、如果空间四个点不共面,则四个点中可能有三个点共线 |
| D、若直线a∥平面α,点P∈α,则过P作a的平行线一定在α内 |
已知双曲线C的方程为x2-
=1,直线l是双曲线C的右准线,F1、F2是双曲线C的左、右焦点,点P在双曲线C上,d为点P到直线l的距离,若|PF1|=2|PF2|2,则
的值是( )
| y2 |
| 3 |
| |PF 1| |
| d |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
若点P在三个顶点坐标分别为C(0,0),A(0,2
),B(2,0)的△ABC内运动,则动点P到顶点A的距离|PA|<2
的概率为( )
| 3 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
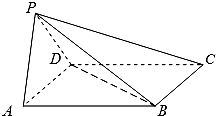 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠BAD=45°,AD=1,AB=
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠BAD=45°,AD=1,AB=