题目内容
观察下列命题
①命题“对任意的x<0,x3-x2+1≤0”的否定是“存在x≥0,x3-x2+1>0”;
②函数f(x)=2x-x2的零点有2个;③若函数f(x)=x2-|x+a|为偶函数,则实数a=0;
④若函数f(x)=
在R上是单调递增函数,则实数a的取值范围为(1,8).
其中真命题的序号是 (写出所有正确命题的编号).
①命题“对任意的x<0,x3-x2+1≤0”的否定是“存在x≥0,x3-x2+1>0”;
②函数f(x)=2x-x2的零点有2个;③若函数f(x)=x2-|x+a|为偶函数,则实数a=0;
④若函数f(x)=
|
其中真命题的序号是
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:①利用命题的否定的意义即可得出;
②利用指数函数和二次函数的性质,画出图象即可得出;
③利用偶函数的定义即可得出;
④利用指数函数、一次函数的单调性、分段函数的意义即可得出.
②利用指数函数和二次函数的性质,画出图象即可得出;
③利用偶函数的定义即可得出;
④利用指数函数、一次函数的单调性、分段函数的意义即可得出.
解答:
解:①命题“对任意的x<0,x3-x2+1≤0”的否定应是“存在x<0,x3-x2+1>0”,因此不正确;
②函数f(x)=2x-x2的图象如图所示,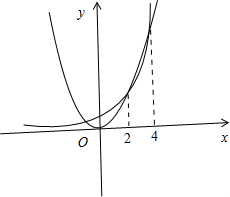 因此函数f(x)的零点应有3个,因此不正确.
因此函数f(x)的零点应有3个,因此不正确.
③若函数f(x)=x2-|x+a|为偶函数,则f(-x)=f(x),
∴|-x+a|=|x+a|对于任意实数x都成立,
解得a=0,因此③正确;
④若函数f(x)=
在R上是单调递增函数,
∴
,解得7≤a<8.
则实数a的取值范围为[7,8).
因此④不正确.
综上可知:只有③正确.
故答案为:③.
②函数f(x)=2x-x2的图象如图所示,
 因此函数f(x)的零点应有3个,因此不正确.
因此函数f(x)的零点应有3个,因此不正确.③若函数f(x)=x2-|x+a|为偶函数,则f(-x)=f(x),
∴|-x+a|=|x+a|对于任意实数x都成立,
解得a=0,因此③正确;
④若函数f(x)=
|
∴
|
则实数a的取值范围为[7,8).
因此④不正确.
综上可知:只有③正确.
故答案为:③.
点评:本题考查了函数的单调性、奇偶性,考查了数形结合的思想方法,属于中档题.

练习册系列答案
相关题目
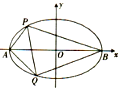 如图,以
如图,以
