题目内容

已知椭圆
x2
a2
+
y2
b2
=1﹙a＞0，b＞0﹚，F1，F2是其左右焦点，若椭圆的离心率为
1
2
，椭圆的焦点到相应准线的距离为3，
（1）求椭圆的标准方程；
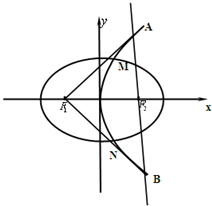
（2）椭圆上是否存在一点M，使点M到其左准线的距离MN是MF1，MF2的等比中项？若存在，求出该点的坐标，若不存在，说明理由．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（1）由题设条件推导出
c
a
=
1
2
a2
c
-c=3
，由此能求出椭圆的标准方程．
（2）解决此类存在性问题是先假设存在适合题意的点，然后进行推理，看能不能推出矛盾．题中涉及到与焦点F1、F2的距离，可考虑应用椭圆的两个定义．
解答： 解：（1）∵椭圆
x2
a2
+
y2
b2
=1﹙a＞0，b＞0﹚，F1，F2是其左右焦点，
椭圆的离心率为
1
2
，椭圆的焦点到相应准线的距离为3，
∴
c
a
=
1
2
a2
c
-c=3
，解得a=2，c=1，∴b=
3
，
∴椭圆的标准方程为
x2
4
+
y2
3
=1．
（2）设|MN|=t（t＞0），由椭圆的第二定义知|MF1|MN=e|MN|=et，
又由椭圆第一定义知|MF1|+|MF2|=2a，
∴|MF2|=2a-et，
若点M存在，则|MN|2=|MF1|•|MF2|，
∴t2=et•（2a-et），
∵t≠0，∴t=
2ae
1+e2
=
2×2×
1
2
1+
1
4
=
8
5
，
∵椭圆C上有点到左准线的最短距离是椭圆左顶点到左准线的距离，
即
a2
c
-a=4-2=2，
而|MN|=t=
8
5
＜2，
∴点M不存在．
点评：本题考查椭圆方程的求法，考查点的存在性问题的确定，解题时要认真审题，注意椭圆的两个定义的灵活运用．
练习册系列答案
相关题目
下列说法中正确的是（　　）
A、“a=1”是直线“l1：ax+2y-1=0与直线l2：x+（a+1）y+4=0平行”的充要条件
B、命题“?x∈R，x2-x＞0”的否定是“?x∈R，x2-x＞0”
C、命题“若m＞0，则方程x2+x-m=0有实数根”的逆否命题为：“若方程x2+x-m=0无实数根，则m≤0”
D、若p∧q为假命题，则p，q均为假命题
“a≥0，b≥0”是“
a+b
2
≥
ab
”的（　　）
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充也不必要条件
在平面直角坐标系中，已知点E（-1，0）和F（1，0），圆E是以E为圆心，半径为2
2
的圆，点P是圆E上任意一点，线段FP的垂直平分线l和半径EP所在的直线交于点Q．
（Ⅰ）当点P在圆上运动时，求点Q的轨迹方程T；
（Ⅱ）已知M，N是曲线T上的两点，若曲线T上存在点P，满足
OM
+
ON
=λ
OP
（O为坐标原点），求实数λ的取值范围．
已知椭圆C的焦点为F1（-1，0）、F2（1，0），点P（-1，
2
2
）在椭圆上．
（1）求椭圆C的方程；
（2）若抛物线E：y2=2px（p＞0）与椭圆C相交于点M、N，当△OMN（O是坐标原点）的面积取得最大值时，求P的值．
（3）在（2）的条件下，过点F2作任意直线l与抛物线E相交于点A、B两点，则直线AF1与直线BF1的斜率之和是否为定值？若是，求出定值；若不是，说明理由．
设函数f（x）=aex（x+1）（其中e=2.71828…），g（x）=x2+bx+2，已知它们在x=0处有相同的切线．
（Ⅰ）求函数f（x），g（x）的解析式；
（Ⅱ）求函数f（x）在[t，t+1]（t＞-3）上的最小值；
（Ⅲ）判断函数F（x）=2f（x）-g（x）+2零点个数．
已知动圆过定点（1，0），且与直线x=-1相切．
（1）求动圆圆心C的轨迹方程；
（2）设A、B是轨迹C上两个不同的点，且OA⊥OB，证明直线AB恒过定点，并求定点的坐标．
如图，以
3
2
为离心率的椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左右顶点分别为A和B，点P是椭圆位于x轴上方的一点，且△PAB的面积最大值为2．
（Ⅰ）求椭圆方程；
（Ⅱ）设点Q是椭圆位于x轴下方的一点，直线AP、BQ的斜率分别为k1，k2，若k1=7k2，设△BPQ与△APQ的面积分别为S1，S2，求S1-S2的最大值．
已知椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)上的顶点为A（0，5），离心率为
3
2
．
（Ⅰ）求椭圆E的方程；
（Ⅱ）若直线y=-4交椭圆E于点B，C两点（点B在点C的左侧），点D在椭圆上，且满足
BD
=m
BA
+n
BC
（m，n为实数），求m+n的最大值以及对应点D的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网