题目内容
已知数列{an}为等比数列,其前n项和为Sn,已知a1+a4=-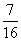 ,且对于任意的n∈N+有Sn,Sn+2,Sn+1成等差数列.
,且对于任意的n∈N+有Sn,Sn+2,Sn+1成等差数列.
(1)求数列{an}的通项公式;
(2)已知bn=n(n∈N+),记Tn=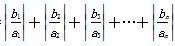 ,若(n-1)2≤m(Tn-n-1)对于n≥2恒成立,求实数m的范围.
,若(n-1)2≤m(Tn-n-1)对于n≥2恒成立,求实数m的范围.
解析:(1)设等比数列{an}的公比为q,
∵ S1,S3,S2成等差数列,
∴ 2S3=S1+S2,
∴ 2a1(1+q+q2)=a1(2+q),得q=-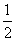 ,
,
又a1+a4=a1(1+q3)=-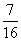 ,
,
∴ a1=-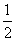 ,∴ an=a1qn-1=
,∴ an=a1qn-1=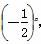
(2)∵ bn=n,an=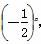
∴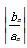 =n·2n,
=n·2n,
∴ Tn=1·2+2·22+3·23+…+n·2n,①
2Tn=1·22+2·23+3·24+…+(n-1)·2n+n·2n+1,②
由①-②,得-Tn=2+22+23+…+2n-n·2n+1,
∴ Tn=-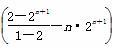 =(n-1)·2n+1+2.
=(n-1)·2n+1+2.
若(n-1)2≤m(Tn-n-1)对于n≥2恒成立,
则(n-1)2≤m[(n-1)·2n+1+2-n-1],
(n-1)2≤m(n-1)·(2n+1-1),
∴ m≥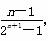 ,
,
令f(n)=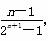 ,f(n+1)-f(n)=
,f(n+1)-f(n)=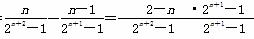 <0,∴ f(n)为减函数,
<0,∴ f(n)为减函数,
∴ f(n)≤f(2)=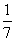 .
.
∴ m≥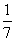 .即m的取值范围是
.即m的取值范围是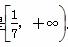 .
.

练习册系列答案
相关题目
 sin x,1),b=(y,cos x),且a∥b.
sin x,1),b=(y,cos x),且a∥b.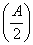 =M,且a=2,求bc的最大值.
=M,且a=2,求bc的最大值.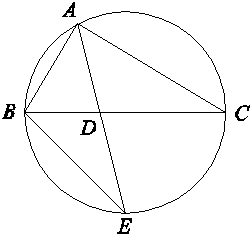
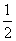 AD·AE,求∠BAC的大小.
AD·AE,求∠BAC的大小. 的范围是__________.
的范围是__________.