题目内容
5.在区间[0,1]上任取两个数,则这两个数之和小于$\frac{8}{5}$的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{16}{25}$ | C. | $\frac{17}{25}$ | D. | $\frac{23}{25}$ |
分析 本题是一个等可能事件的概率,试验发生包含的事件是在区间[0,1]上任取两个数a和b,写出事件对应的集合,做出面积,满足条件的事件是a+b<$\frac{8}{5}$,写出对应的集合,做出面积,得到概率.
解答 解:由题意知本题是一个等可能事件的概率,
∵试验发生包含的事件是在区间[0,1]上任取两个数a和b,
事件对应的集合是Ω={(a,b)|0≤a≤1,0≤b≤1}
对应的面积是sΩ=1
满足条件的事件是a+b<$\frac{8}{5}$,事件对应的集合是A={(a,b)|0≤a≤1,0≤b≤1,a+b<$\frac{8}{5}$}
对应的图形的面积是sA=1-$\frac{1}{2}×\frac{2}{5}×\frac{2}{5}$=1-$\frac{2}{25}$=$\frac{23}{25}$
∴根据等可能事件的概率得到P=$\frac{23}{25}$,
故选D.
点评 本题考查等可能事件的概率,是一个几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到结果,是一个基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.若向量$\vec a=(1,λ,2),\vec b=(2,-1,2)$,且$\vec a$与$\vec b$的夹角余弦为$\frac{8}{9}$,则λ等于( )
| A. | -2或$\frac{2}{55}$ | B. | -2 | C. | 2 | D. | 2或$-\frac{2}{55}$ |
20.数列{an}满足a1=$\frac{4}{3}$,an+1-1=an(an-1)(n∈N*),且Sn=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$,则Sn的整数部分的所有可能值构成的集合是( )
| A. | {0,1,2} | B. | {0,1,2,3} | C. | {1,2} | D. | {0,2} |
17.直线l的方程为2x-y=0是“直线l平分圆(x-1)2+(y-2)2=1的周长”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
14.若复数z满足z•i=2+3i,则在复平面内z对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
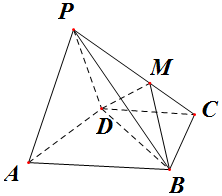 如图,在四棱锥P-ABCD中,AB∥CD,△PAD是等边三角形,平面PAD⊥平面ABCD,已知AD=2,$BD=2\sqrt{3}$,AB=2CD=4.
如图,在四棱锥P-ABCD中,AB∥CD,△PAD是等边三角形,平面PAD⊥平面ABCD,已知AD=2,$BD=2\sqrt{3}$,AB=2CD=4.