题目内容
10.已知数列{an}与{bn}满足${a_{n+1}}+2{b_n}=2{b_{n+1}}+{a_n}({n∈{N^*}})$,若${a_1}=9,{b_n}={3^n}$(n∈N*)且$λ{a_n}>{3^n}+36({n-3})+3λ$对一切n∈N*恒成立,则实数λ的取值范围是($\frac{13}{18}$,+∞).分析 化简条件式得an+1-an=4•3n,使用累加法求出an的通项公式,代入条件式得出λ>$\frac{1}{2}$+$\frac{18(n-3)}{{3}^{n}}$.利用数列的单调性得出右侧数列的最大值即可得出λ的范围.
解答 解:∵bn=3n,∴bn+1=3n+1,代入${a_{n+1}}+2{b_n}=2{b_{n+1}}+{a_n}({n∈{N^*}})$,化简得an+1-an=2(bn+1-bn)=4•3n,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=4(3n-1+3n-2+…+3)+9=2•3n+3.
故$λ{a_n}>{3^n}+36({n-3})+3λ$可化为λ>$\frac{1}{2}$+$\frac{18(n-3)}{{3}^{n}}$.
令cn=$\frac{1}{2}$+$\frac{18(n-3)}{{3}^{n}}$,则cn-cn-1=$\frac{18(n-3)}{{3}^{n}}$-$\frac{18(n-4)}{{3}^{n-1}}$=$\frac{18(9-2n)}{{3}^{n}}$,
∴当n≥5,{cn}单调递减,当1<n≤4时,{cn}单调递增,
∴当n=4时cn取得最大值c4=$\frac{1}{2}+$$\frac{2}{9}$=$\frac{13}{18}$,
∴λ>$\frac{13}{18}$.
故答案为($\frac{13}{18}$,+∞).
点评 本题考查了数列的递推公式,数列通项的求法,数列最值的计算,属于中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
20.已知椭圆M:(x-2)2+y2=4,则过点(1,1)的直线中被圆M截得的最短弦长为2$\sqrt{2}$.类比上述方法:设球O是棱长为3的正方体ABCD-A1B1C1D1的外接球,过AC1的一个三等分点作球O的截面,则最小截面的面积为( )
| A. | π | B. | 4π | C. | 5π | D. | 6π |
1.在△ABC中,AB=2,BC=$\sqrt{10}$,cosA=$\frac{1}{4}$,则AB边上的高等于( )
| A. | $\frac{3\sqrt{15}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{3\sqrt{15}}{2}$ | D. | 3 |
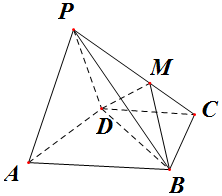 如图,在四棱锥P-ABCD中,AB∥CD,△PAD是等边三角形,平面PAD⊥平面ABCD,已知AD=2,$BD=2\sqrt{3}$,AB=2CD=4.
如图,在四棱锥P-ABCD中,AB∥CD,△PAD是等边三角形,平面PAD⊥平面ABCD,已知AD=2,$BD=2\sqrt{3}$,AB=2CD=4.