题目内容
设二次函数f(x)=ax2+bx+c(a、b、c∈Z),已知方程f(x)=0在区间(-2,0)内有两个不等的实根,且对任意实数x恒有4x+2≤f(x)≤8x2+12x+4,求a、b、c的值.
考点:函数恒成立问题
专题:函数的性质及应用
分析:根据不等式恒成立,先确定c的取值范围,以及x=-
是方程f(x)=0的一个根,建立a,b,c的关系,进而得到a,b,c的取值,然后验证即可得到结论.
| 1 |
| 2 |
解答:
解:∵对任意实数x恒有4x+2≤f(x)≤8x2+12x+4,
∴当x=0时,不等式等价为2≤f(0)≤4,
即2≤c≤4,
当x=-
时,不等式等价为0≤f(-
)≤0,
即x=-
是方程f(x)=0的一个根,
即
a-
b+c=0,
即b=
a+2c.①
设g(x)=4x+2,h(x)=8x2+12x+4,
则g(-
)=0,h(-
)=0,
∴g'(x)=4,h'(x)=16x+12.
g'(-
)=4,h'(-
)=4,
即g(x)=4x+2是h(x)=8x2+12x+4在x=-
处的切线,
∴g(x)=4x+2也是f(x)=ax2+bx+c在x=-
处的切线,
即f'(x)=2ax+b在x=-
处的切线斜率k=f'(-
)=4=-a+b,②,
由①②得
,
即
,
∵2≤c≤4,
∴当c=2时,a=0不成立.
当c=3时,a=4,b=8,此时f(x)=4x2+8x+3=(2x+1)(2x+3).在区间(-2,0)内有两个不相等的实根x=-
或x=-
,满足条件.
当c=4时,a=8,b=12,此时f(x)=8x2+12x+4=4(2x+1)(x+1).在区间(-2,0)内有两个不相等的实根x=-
或x=-1,满足条件.
∴a=4,b=8,c=3或a=8,b=12,c=4.
∴当x=0时,不等式等价为2≤f(0)≤4,
即2≤c≤4,
当x=-
| 1 |
| 2 |
| 1 |
| 2 |
即x=-
| 1 |
| 2 |
即
| 1 |
| 4 |
| 1 |
| 2 |
即b=
| 1 |
| 2 |
设g(x)=4x+2,h(x)=8x2+12x+4,
则g(-
| 1 |
| 2 |
| 1 |
| 2 |
∴g'(x)=4,h'(x)=16x+12.
g'(-
| 1 |
| 2 |
| 1 |
| 2 |
即g(x)=4x+2是h(x)=8x2+12x+4在x=-
| 1 |
| 2 |
∴g(x)=4x+2也是f(x)=ax2+bx+c在x=-
| 1 |
| 2 |
即f'(x)=2ax+b在x=-
| 1 |
| 2 |
| 1 |
| 2 |
由①②得
|
即
|
∵2≤c≤4,
∴当c=2时,a=0不成立.
当c=3时,a=4,b=8,此时f(x)=4x2+8x+3=(2x+1)(2x+3).在区间(-2,0)内有两个不相等的实根x=-
| 1 |
| 2 |
| 3 |
| 2 |
当c=4时,a=8,b=12,此时f(x)=8x2+12x+4=4(2x+1)(x+1).在区间(-2,0)内有两个不相等的实根x=-
| 1 |
| 2 |
∴a=4,b=8,c=3或a=8,b=12,c=4.
点评:本题主要考查不等式恒成立,利用二次函数的图象和性质是解决本题的关键,考查学生的计算能力.

练习册系列答案
相关题目
下列说法正确的是( )
| A、?x0∈R,ex0≤0 | ||
| B、对?a>b,则ab=2,(a2+b2)min=4 | ||
| C、a>1,b>1是ab>1的充分条件 | ||
D、a+b=0的充要条件是
|
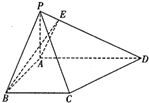 在四棱锥P-ABCD中,底面ABCD是一直角梯,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,PA⊥底面ABCD,PD与底面成30°角.
在四棱锥P-ABCD中,底面ABCD是一直角梯,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,PA⊥底面ABCD,PD与底面成30°角.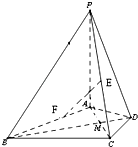 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.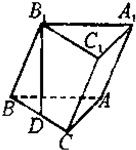 如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠C=90°,侧棱与底面所成的角为α(0°<α<90°),点B1在底面上的射影D落在BC上.
如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠C=90°,侧棱与底面所成的角为α(0°<α<90°),点B1在底面上的射影D落在BC上.