题目内容
设各项均为正数的数列{an}和{bn}满足：an，bn，an+1成等差数列，bn，an+1，bn+1成等比数列，且a1=1，b1=2，a2=3，求通项an，bn．
考点：等比数列的性质,等差数列的性质
专题：等差数列与等比数列
分析：利用等差数列的定义证明数列{
}是等差数列．再利用等差数列的通项公式求出
的通项公式，进而求出bn，an．
| bn |
| bn |
解答：
解：∵an，bn，an+1成等差数列，bn，an+1，bn+1成等比数列
∴2bn=an+an+1①，
an+12=bn•bn+1②．
由②得an+1=
③．
将③代入①得，对任意n≥2，n∈N*，
有2bn=
+
．
∵bn＞0，
∴2
=
+
，
∴{
}是等差数列．
设数列{
}的公差为d，
由a1=1，b1=2，a2=3，得b2=
．
∴
=
，
=
，
d=
．
∴
=
，
∴bn=
．
an=
=
．
∴2bn=an+an+1①，
an+12=bn•bn+1②．
由②得an+1=
| bnbn+1 |
将③代入①得，对任意n≥2，n∈N*，
有2bn=
| bn-1bn |
| bnbn+1 |
∵bn＞0，
∴2
| bn |
| bn-1 |
| bn+1 |
∴{
| bn |
设数列{
| bn |
由a1=1，b1=2，a2=3，得b2=
| 9 |
| 2 |
∴
| b1 |
| 2 |
| b2 |
3
| ||
| 2 |
d=
| ||
| 2 |
∴
| bn |
| n+1 |
| 2 |
| 2 |
∴bn=
| (n+1)2 |
| 2 |
an=
| bn-1bn |
| n(n+1) |
| 2 |
点评：本题考查了等差、等比数列的通项公式，利用构造等差数列法求得数列{
}的通项公式是解答本题的突破口，本题还考查了学生的运算能力，运算要细心．
| bn |
练习册系列答案
相关题目
下列说法不正确的是（ ）
| A、所有的对立事件都是互斥事件 | ||
B、先后抛掷两枚大小一样的硬币，两枚都出现反面的概率是
| ||
| C、事件“直线y=k（x+1）过点（-1，0）”是必然事件 | ||
D、某红绿灯路口，红灯时间为30秒，黄灯时间为5秒，绿灯时间为45秒，当你到这个路口时，看到黄灯的概率是
|
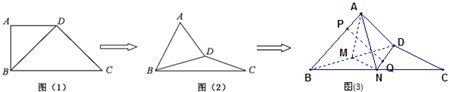在直角梯形ABCD中，AD∥BC，
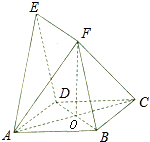如图，四边形ABCD与BDEf均为菱形，已知∠DAB=∠DBF=60°，且面ABCD⊥面BDEF，AC=2