题目内容

若不等式
3x2+2x+2
x2+x+1
≥m对于任意的实数x均成立，求自然数m的值．
考点：函数恒成立问题
专题：综合题,函数的性质及应用
分析：不等式
3x2+2x+2
x2+x+1
≥m对于任意的实数x均成立，等价于（m-3）x2+（m-2）x+m-2≤0对于任意的实数x均成立，分类讨论，利用根的判别式即可求得m的取值范围．
解答： 解：不等式
3x2+2x+2
x2+x+1
≥m对于任意的实数x均成立，等价于（m-3）x2+（m-2）x+m-2≤0对于任意的实数x均成立．
m=3时，x+1≤0，∴x≤-1，不满足题意；
m≠3时，
m-3＜0
(m-2)2-4(m-3)(m-2)≤0
，∴m≤2，
∴自然数m的值为0，1，2．
点评：本题考查二次函数在R中的恒成立问题，可以通过判别式法予以解决，也可以分离参数m，分类讨论解决
练习册系列答案
相关题目
设递增等比数列{an}的前n项和为Sn，且a2=3，S3=13，数列{bn}满足b1=a1，点P（bn，bn+1）在直线x-y+2=0上，n∈N*．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）设cn=
bn
an
，数列{cn}的前n项和Tn，若Tn＞2a-1恒成立（n∈N*），求实数a的取值范围．
已知f(x)=ln(x+1) ， g(x)=
1
2
ax2+bx (a，b∈R)．
（1）若b=2且h（x）=f（x-1）-g（x）存在单调递减区间，求实数a的取值范围；
（2）若a=0，b=1，求证：当x∈（-1，+∞）时，f（x）-g（x）≤0恒成立；
（3）设x＞0，y＞0，证明：xlnx+ylny＞(x+y)ln
x+y
2
．
设二次函数f（x）=ax2+bx+c（a、b、c∈Z），已知方程f（x）=0在区间（-2，0）内有两个不等的实根，且对任意实数x恒有4x+2≤f（x）≤8x2+12x+4，求a、b、c的值．
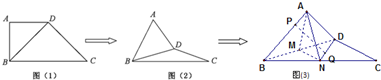在直角梯形ABCD中，AD∥BC，BC=2AD=2AB=2
2
，∠ABC=90°（如图1）．把△ABD沿BD翻折，使得二面角A-BD-C的平面角为θ（如图2）
（1）若θ=
π
2
，求证：CD⊥AB；
（2）是否存在适当θ的值，使得AC⊥BD，若存在，求出θ的值，若不存在说明理由；
（3）取BD中点M，BC中点N，P、Q分别为线段AB与DN上一点，使得
AP
PB
=
NQ
QD
=λ(λ∈R)．令PQ与BD和AN所成的角分别为θ1和θ2．求证：对任意θ∈（0．π），总存在实数λ，使得sinθ1+sinθ2均存在一个不变的最大值．并求出此最大值和取得最大值时θ与λ的关系．
已知函数f（x）=x+
a
x
，g（x）=x2-bx a、b∈R．
（1）若集合{x|f（x）=2x+2}只含有一个元素，试求实数a的值；
（2）在（1）的条件下，当m∈[2，4]，n∈[1，5]时有f（m）大于等于g（n）恒成立，试求实数b的取值范围．
已知函数f（x）=Asin（ωx+
π
6
）（x∈R，A＞0，ω＞0）的最小正周期为T=6π，且f（2π）=2
（1）求ω和A的值；
（2）设α，β∈[0，
π
2
]，f（3α+π）=
16
5
，f（3β+
5π
2
）=-
20
13
，求cos（α-β）．
若直线ax-by+1=0平分圆C：x2+y2+2x-4y+1=0的周长，则ab的取值范围是
 
．
设函数y=f（x）是定义域为R，周期为2的周期函数，且当x∈[-1，1）时，f（x）=1-x2；已知函数g（x）=
lg|x|，x≠0
1，x=0
，则函数f（x）和g（x）的图象在区间[-5，10]内公共点的个数为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网