题目内容
下列说法正确的是( )
| A、?x0∈R,ex0≤0 | ||
| B、对?a>b,则ab=2,(a2+b2)min=4 | ||
| C、a>1,b>1是ab>1的充分条件 | ||
D、a+b=0的充要条件是
|
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.?x∈R,则ex>0,即可判断出?x0∈R,ex0≤0是否正确;
B.对?a>b,则ab=2,(a2+b2)min>4;
C.由a>1,b>1可得ab>1;反之不一定成立:例如取a=-2,b=-3,则ab>1.
D.a+b=0的充要条件是
=-1或a=b=0.
B.对?a>b,则ab=2,(a2+b2)min>4;
C.由a>1,b>1可得ab>1;反之不一定成立:例如取a=-2,b=-3,则ab>1.
D.a+b=0的充要条件是
| a |
| b |
解答:
解:A.?x∈R,则ex>0,因此?x0∈R,ex0≤0不正确;
B.对?a>b,则ab=2,(a2+b2)min>4,因此B不正确;
C.由a>1,b>1可得ab>1;反之不一定成立:例如取a=-2,b=-3,则ab>1.
因此a>1,b>1是ab>1的充分不必要条件,因此正确;
D.a+b=0的充要条件是
=-1或a=b=0,因此不正确.
综上可知:只有C正确.
故选:C.
B.对?a>b,则ab=2,(a2+b2)min>4,因此B不正确;
C.由a>1,b>1可得ab>1;反之不一定成立:例如取a=-2,b=-3,则ab>1.
因此a>1,b>1是ab>1的充分不必要条件,因此正确;
D.a+b=0的充要条件是
| a |
| b |
综上可知:只有C正确.
故选:C.
点评:本题综合考查了指数函数的性质、重要不等式与基本不等式、充分必要条件等基础知识,属于基础题.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
下列说法不正确的是( )
| A、所有的对立事件都是互斥事件 | ||
B、先后抛掷两枚大小一样的硬币,两枚都出现反面的概率是
| ||
| C、事件“直线y=k(x+1)过点(-1,0)”是必然事件 | ||
D、某红绿灯路口,红灯时间为30秒,黄灯时间为5秒,绿灯时间为45秒,当你到这个路口时,看到黄灯的概率是
|
下列命题中的假命题是( )
| A、?x∈R,2x-1>0 |
| B、?x∈R,lgx<1 |
| C、?x∈N+,(x-1)2>0 |
| D、?x∈R,tanx=2 |
已知集合A={x||x+1|<1},B={x|y=
,y∈R},则A∩∁RB=( )
(
|
| A、(-2,1) |
| B、(-2,-1] |
| C、(-1,0) |
| D、[-1,0) |
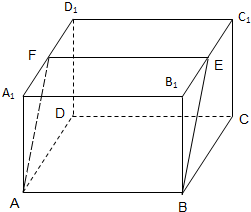 如图,直四棱柱ABCD-A1B1C1D1的底面边长为2的菱形,∠BAD=60°,高为1,过底边AB作一截面ABEF,若BE=2
如图,直四棱柱ABCD-A1B1C1D1的底面边长为2的菱形,∠BAD=60°,高为1,过底边AB作一截面ABEF,若BE=2 如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=2AB.
如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=2AB.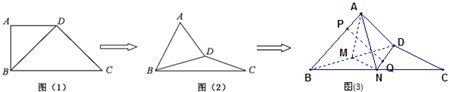 在直角梯形ABCD中,AD∥BC,
在直角梯形ABCD中,AD∥BC,