题目内容
已知在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,各棱长均为3,P、Q分别是侧棱BB1、CC1上的点,且BP=C1Q=1.
(1)在AC上是否存在一点D,使得BD∥平面APQ?证明你的结论;
(2)利用(1)的结论证明:平面APQ⊥平面AA1CC1;
(3)求三棱柱Q-APA1的体积.
(1)在AC上是否存在一点D,使得BD∥平面APQ?证明你的结论;
(2)利用(1)的结论证明:平面APQ⊥平面AA1CC1;
(3)求三棱柱Q-APA1的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)当D为AC中点时,BD∥平面APQ.由已知得BP=C1Q=1,取AQ中点E,连结PE、ED,则四边形BDEP是平行四边形由此能证明BD∥平面APQ.
(2)由已知得平面ABC⊥平面AA1C1C,BD⊥平面AA1C1C,PE⊥平面AA1C1C,由此能证明面APQ⊥面AA1C1C.
(3)由VQ-APA1=VP-QAA1,利用等积法能求出三棱柱Q-APA1的体积.
(2)由已知得平面ABC⊥平面AA1C1C,BD⊥平面AA1C1C,PE⊥平面AA1C1C,由此能证明面APQ⊥面AA1C1C.
(3)由VQ-APA1=VP-QAA1,利用等积法能求出三棱柱Q-APA1的体积.
解答:
(1)解:当D为AC中点时,BD∥平面APQ.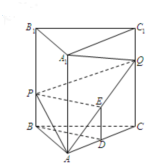
证明如下:
∵三棱柱ABC-A1B1C1中,AA1⊥平面ABC,各棱长均为3,
∴BP=C1Q=1,P,Q分别是BB1,CC1上的三等分点,
取AQ中点E,连结PE、ED,则DE为△AQC的中位线,
∴ED∥CQ,ED=
CQ,
又∵BP∥QC,BP=
QC,∴BP∥DE,BP=DE,
∴四边形BDEP是平行四边形,∴PE∥BD,
∵PE?平面APQ,BD?平面APQ,
∴BD∥平面APQ.
(2)证明:∵AA1⊥平面ABC,∴平面ABC⊥平面AA1C1C,
∵BD⊥AC,BD?平面ABC,平面ABC∩平面AA1C1C=AC,
∴BD⊥平面AA1C1C,
∴四边形BDEP是平行四边形,∴PE∥BD,
∴PE⊥平面AA1C1C,
∵PE?平面APQ,∴平面APQ⊥平面AA1C1C.
(3)解:VQ-APA1=VP-QAA1=
×PE×S△OAA1
=C
=
×
×
×3×3
=
.

证明如下:
∵三棱柱ABC-A1B1C1中,AA1⊥平面ABC,各棱长均为3,
∴BP=C1Q=1,P,Q分别是BB1,CC1上的三等分点,
取AQ中点E,连结PE、ED,则DE为△AQC的中位线,
∴ED∥CQ,ED=
| 1 |
| 2 |
又∵BP∥QC,BP=
| 1 |
| 2 |
∴四边形BDEP是平行四边形,∴PE∥BD,
∵PE?平面APQ,BD?平面APQ,
∴BD∥平面APQ.
(2)证明:∵AA1⊥平面ABC,∴平面ABC⊥平面AA1C1C,
∵BD⊥AC,BD?平面ABC,平面ABC∩平面AA1C1C=AC,
∴BD⊥平面AA1C1C,
∴四边形BDEP是平行四边形,∴PE∥BD,
∴PE⊥平面AA1C1C,
∵PE?平面APQ,∴平面APQ⊥平面AA1C1C.
(3)解:VQ-APA1=VP-QAA1=
| 1 |
| 3 |
=C
=
| 1 |
| 3 |
3
| ||
| 3 |
| 1 |
| 2 |
=
9
| ||
| 4 |
点评:本题考查使得BD∥平面APQ的点D的位置的判断与证明,考查平面APQ⊥平面AA1CC1的证明,考查三棱柱Q-APA1的体积的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
若实数x,y满足x+y+(x-y)i=2,则xy的值是( )
| A、1 | B、2 | C、-2 | D、-3 |
“a≠2”是“关于x,y的二元一次方程组
有唯一解”的( )
|
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
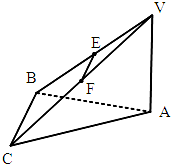 如图,在三棱锥V-ABC中,点E、F分别为VB、VC的中点.平面VAB⊥平面ABC,平面VAC⊥平面ABC.
如图,在三棱锥V-ABC中,点E、F分别为VB、VC的中点.平面VAB⊥平面ABC,平面VAC⊥平面ABC.