题目内容
设集合M={x|x2+2(1-a)x+3-a≤0,x∈R},M⊆[0,3],求实数a的取值范围.
考点:集合的包含关系判断及应用
专题:集合
分析:当M⊆[0,3],通过f(0)≥0,且f(3)≥0,以及对应的二次函数的对称轴的范围,即可求实数a的取值范围.
解答:
解:设y=x2+2(1-a)x+3-a,其开口向上,
那么满足y=x2+2(1-a)x+3-a≤0,的x的取值,
即为使 二次函数在x轴下方 的x的取值范围,
也就是 二次函数与y轴交点 之间的部分,
当M包含于[0,3]时,
二次函数与y轴两交点之间的部分,或M为空集,应包含于区间[0,3]之间,
即 两交点都在[0,3]之间,
可知 f(0)≥0,f(3)≥0,且0≤a-1≤3
f(0)=3-a≥0,a≤3
f(3)=9+6(1-a)+(3-a)=18-7a≥0,a≤
,
0≤a-1≤3⇒1≤a≤4
综上1≤a≤
.
那么满足y=x2+2(1-a)x+3-a≤0,的x的取值,
即为使 二次函数在x轴下方 的x的取值范围,
也就是 二次函数与y轴交点 之间的部分,
当M包含于[0,3]时,
二次函数与y轴两交点之间的部分,或M为空集,应包含于区间[0,3]之间,
即 两交点都在[0,3]之间,
可知 f(0)≥0,f(3)≥0,且0≤a-1≤3
f(0)=3-a≥0,a≤3
f(3)=9+6(1-a)+(3-a)=18-7a≥0,a≤
| 18 |
| 7 |
0≤a-1≤3⇒1≤a≤4
综上1≤a≤
| 18 |
| 7 |
点评:本题是中档题,考查集合的运算,构造法与函数的零点与方程的根的知识,考查计算能力,转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
直线l过点A(3,1)与x轴正向、y轴正向分别交于M、N两点,则|MA|•|NA|的最小值为( )
| A、2 | B、4 | C、6 | D、8 |
下列命题是真命题的是( )
| A、-1的平方根只有一个 |
| B、i是1的四次方根 |
| C、i是-1的立方根 |
| D、i是方程x2-1的根 |
若实数x,y满足x+y+(x-y)i=2,则xy的值是( )
| A、1 | B、2 | C、-2 | D、-3 |
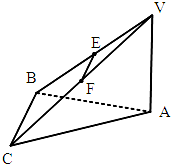 如图,在三棱锥V-ABC中,点E、F分别为VB、VC的中点.平面VAB⊥平面ABC,平面VAC⊥平面ABC.
如图,在三棱锥V-ABC中,点E、F分别为VB、VC的中点.平面VAB⊥平面ABC,平面VAC⊥平面ABC.