题目内容
已知函数f（x）=asin（x-1）+bx+c（a∈R，b，c∈Z），对于取定的一组a，b，c的值，若计算得到f（-1）=1，则f（3）的值一定不可能是（ ）
| A、5 | B、-2 | C、1 | D、-3 |
考点：函数的值
专题：函数的性质及应用
分析：求出f（1）和f（-1），求出它们的和；由于c∈Z，判断出f（1）+f（-1）为偶数．
解答：
解：f（1）=asin1+b+c ①
f（-1）=-asin1-b+c ②
①+②得：
f（1）+f（-1）=2c，
∵c∈Z，
∴f（1）+f（-1）是偶数
∵f（-1）=1，
∴f（3）的值一定是奇数，
故选：B
f（-1）=-asin1-b+c ②
①+②得：
f（1）+f（-1）=2c，
∵c∈Z，
∴f（1）+f（-1）是偶数
∵f（-1）=1，
∴f（3）的值一定是奇数，
故选：B
点评：本题考查知函数的解析式求函数值、考查偶数的特点．
练习册系列答案
相关题目
已知二次函数的图象如图所示，则其导函数f′（x）的图象大致形状是（ ）
A、 |
B、 |
C、 |
D、 |
若实数x，y满足x+y+（x-y）i=2，则xy的值是（ ）
| A、1 | B、2 | C、-2 | D、-3 |
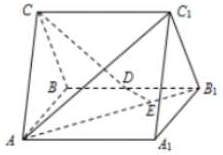如图，直三棱柱ABC-A1B1C1中，AC=BC，C到AB的距离大于1，AA1=AB=2，D为BB1的中点，E为AB1上的一点，AE=3EB1．
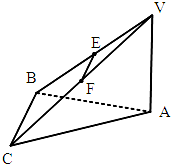如图，在三棱锥V-ABC中，点E、F分别为VB、VC的中点．平面VAB⊥平面ABC，平面VAC⊥平面ABC．