题目内容
已知集合A={x|3≤3x≤27},B={x|log3x>1}
(1)分别求A∩B,(∁RB)∪A;
(2)已知集合C={x|1<x<a},C?A,求实数a的取值范围.
(1)分别求A∩B,(∁RB)∪A;
(2)已知集合C={x|1<x<a},C?A,求实数a的取值范围.
考点:集合的包含关系判断及应用,交、并、补集的混合运算
专题:集合
分析:首先化简集合A,B,然后解答.
解答:
解:由已知A={x|3≤3x≤27}={x|1≤x≤3},B={x|log3x>1}={x|x>3},
所以(1)A∩B=∅,(∁RB)∪A={x|x≤3}∪{x|1≤x≤3}={x|x≤3};
(2)集合C={x|1<x<a},C?A,所以a≤3.
所以实数a的取值范围a≤3.
所以(1)A∩B=∅,(∁RB)∪A={x|x≤3}∪{x|1≤x≤3}={x|x≤3};
(2)集合C={x|1<x<a},C?A,所以a≤3.
所以实数a的取值范围a≤3.
点评:本题考查了指数函数、对数函数的单调性的运用以及集合的运算,关键是正确化简集合,然后由进行集合的运算,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,角A,B,C所对的边长分别为a,b,c,若sin(A+
)=1且
=
,则∠C等于( )
| π |
| 3 |
| b |
| a |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知m和n是两条不同的直线,α和β是两个不重合的平面,则下列给出的条件中,一定能推出m⊥β的是( )
| A、α⊥β且m?α |
| B、α⊥β且m∥α |
| C、m∥n且n⊥β |
| D、m⊥n且n∥β; |
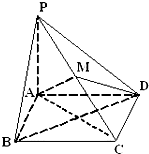 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,PA=1,点M是棱PC上的一点,且AM⊥PB.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,PA=1,点M是棱PC上的一点,且AM⊥PB.