题目内容
5．已知点A（3，6），在x轴上的点P与点A的距离等于10，求点P的坐标．分析 设出P的坐标，利用距离公式列出方程求解即可．
解答 解：设点P（x，0），
由题意可得：$\sqrt{（x-3）^{2}+（{0-6）}^{2}}$=10，解得x=11或x=-5，
点P的坐标：（11，0）或（-5，0）．
点评 本题考查两点间距离公式的应用，考查计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．已知x是非零实数，则“x＞1”是“$\frac{1}{x}$＜1”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
16．
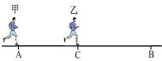如图所示，甲从A地由静止匀加速跑向B地，当甲前进距离为x1时，乙从距A地x2处的C点由静止出发，加速度与甲相同，最后二人同时到达B地，则AB两地距离为（ ）
如图所示，甲从A地由静止匀加速跑向B地，当甲前进距离为x1时，乙从距A地x2处的C点由静止出发，加速度与甲相同，最后二人同时到达B地，则AB两地距离为（ ）| A． | x1+x2 | B． | $\frac{（{x}_{1}+{x}_{2}）^{2}}{4{x}_{1}}$ | ||
| C． | $\frac{{x}_{1}^{2}}{4（{x}_{1}+{x}_{2}）}$ | D． | $\frac{（{x}_{1}+{x}_{2}）^{2}}{（{x}_{1}-{x}_{2}）{x}_{1}}$ |
10．已知集合A={x|y=$\sqrt{x+1}$}，B={y|y＜1}，则A∩B=（ ）
| A． | （-1，1） | B． | [-1，1] | C． | [-1，1） | D． | （-∞，-1]∪[1，+∞） |