题目内容
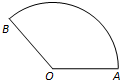 如图,扇形OAB中,OA=OB=1,
如图,扇形OAB中,OA=OB=1, |
| AB |
 |
| AB |
A、1-
| ||
B、2-
| ||
C、1-
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:求出∠AOC和∠BOC中为直角的位置,利用几何概型的概率公式即可得到结论.
解答:
 解:∵扇形OAB中,OA=OB=1,
解:∵扇形OAB中,OA=OB=1,
=2.
∴∠A0B=
=2弧度,
过O分别作OE⊥AO,OD⊥OB,
则∠BOE=∠AOD=2-
,
当点C位于弧BE,或AD上时,∠AOC和∠BOC中至少有一个是钝角,
此时对应的概率P=
=2-
,
故选:B.
 解:∵扇形OAB中,OA=OB=1,
解:∵扇形OAB中,OA=OB=1, |
| AB |
∴∠A0B=
| 2 |
| 1 |
过O分别作OE⊥AO,OD⊥OB,
则∠BOE=∠AOD=2-
| π |
| 2 |
当点C位于弧BE,或AD上时,∠AOC和∠BOC中至少有一个是钝角,
此时对应的概率P=
2(2-
| ||
| 2 |
| π |
| 2 |
故选:B.
点评:本题主要考查几何概型的概率计算,求出∠AOC和∠BOC中至少有一个是钝角的等价条件是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
从12个产品(其中10个是正品,2个是次品)中任意抽取3个.给出下列四个事件:①3个都是正品;②至少有1个是次品;③3个都是次品;④至少有1个是正品,其中为随机事件的是( )
| A、①② | B、①③ | C、②③ | D、②④ |
在△ABC中,cos2
=
(a,b,c分别是角A,B,C的对边),则△ABC的形状为( )
| A |
| 2 |
| b+c |
| 2c |
| A、等腰直角三角形 |
| B、直角三角形 |
| C、等腰三角形或直角三角形 |
| D、等边三角形 |
如图,AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,则
=( )
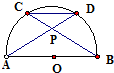
| CD |
| AB |

| A、sinα | ||
| B、cosα | ||
| C、tanα | ||
D、
|
在等差数列{an}中,若a3+a6+a9=90,则S11等于( )
| A、270 | B、300 |
| C、330 | D、360 |
在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )
| A、120° | B、100° |
| C、80° | D、60° |
在等差数列{an}中,a1=-2014,其前n项和为Sn,若
-
=2,则S2014的值为( )
| S12 |
| 12 |
| S10 |
| 10 |
| A、-2011 |
| B、-2012 |
| C、-2013 |
| D、-2014 |
已知命题p:函数y=x3为R上的奇函数;命题q:若b2=ac,则a,b,c一定成等比数列.下列说法正确的是( )
| A、p或q为假 |
| B、p且q为真 |
| C、¬p且q为真 |
| D、¬p或q为假 |