题目内容
过圆C:x2+y2-2x-2y+1=0外一点P所做的圆的两条切线成90°角,求线段PC的中点Q的轨迹方程.
考点:轨迹方程
专题:计算题,直线与圆
分析:将圆C的方程化为标准方程,求出PC=
,可得线段PC的中点Q的轨迹是以(1,1)为圆心,
为半径的圆,即可得出结论.
| 2 |
| ||
| 2 |
解答:
解:圆C:x2+y2-2x-2y+1=0可化为圆(x-1)2+(y-1)2=1,
∵过圆C:x2+y2-2x-2y+1=0外一点P所做的圆的两条切线成90°角,
∴PC=
,
∴线段PC的中点Q的轨迹是以(1,1)为圆心,
为半径的圆,
方程为(x-1)2+(y-1)2=
.
∵过圆C:x2+y2-2x-2y+1=0外一点P所做的圆的两条切线成90°角,
∴PC=
| 2 |
∴线段PC的中点Q的轨迹是以(1,1)为圆心,
| ||
| 2 |
方程为(x-1)2+(y-1)2=
| 1 |
| 2 |
点评:本题考查轨迹方程,确定线段PC的中点Q的轨迹是以(1,1)为圆心,
为半径的圆是关键.
| ||
| 2 |

练习册系列答案
相关题目
在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )
| A、120° | B、100° |
| C、80° | D、60° |
“0<k<2”是“
+
=1表示椭圆”的( )
| x2 |
| 2 |
| y2 |
| k |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
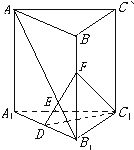 如图,直三棱柱ABC-A1B1C1中,已知AC=BC=AA1=a,∠ACB=90°,D是A1B1中点.
如图,直三棱柱ABC-A1B1C1中,已知AC=BC=AA1=a,∠ACB=90°,D是A1B1中点.
 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=