题目内容
1．
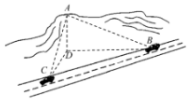如图，小明同学在山顶A处观测到，一辆汽车在一条水平的公路上沿直线匀速行驶，小明在A处测得公路上B，C两点的俯角分别为30°，45°，且∠BAC=135°．若山高AD=100m，汽车从B点到C点历时14s，则这辆汽车的速度为22.6m/s（精确到0.1）参考数据：$\sqrt{2}$≈1.414，$\sqrt{5}$≈2.236．
分析 求出AB=200m，AC=100m，由余弦定理可得BC，即可得出结论．
解答 解：由题意，AB=200m，AC=100$\sqrt{2}$m，
由余弦定理可得BC=$\sqrt{40000+20000-2×200×100\sqrt{2}×（-\frac{\sqrt{2}}{2}）}$≈316.2m
这辆汽车的速度为316.2÷14≈22.6m/s
故答案为：22.6．
点评 本题考查了正弦定理在解三角形中的应用，属于基础题．
练习册系列答案
相关题目
11．下列命题中为真命题的是（ ）
| A． | 若x≠0，则x+$\frac{1}{x}$≥2 | |
| B． | 若直线x-ay=0与直线x-ay=0互相垂直，则a=1 | |
| C． | 命题：“若x2=1，则x=1或x=-1”的逆否命题为：“若x≠1，且x≠-1，则x2≠1” | |
| D． | 一个命题的否命题为真，则它的逆否命题一定为真 |
12．已知球O的半径为2，四点S、A、B、C均在球O的表面上，且SC=4，AB=$\sqrt{3}$，∠SCA=∠SCB=$\frac{π}{6}$，则点B到平面SAC的距离为（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | 1 |
9．要得到函数f（x）=cos2x的图象，只需将函数g（x）=sin2x的图象（ ）
| A． | 向左平移$\frac{1}{2}$个周期 | B． | 向右平移$\frac{1}{2}$个周期 | ||
| C． | 向左平移$\frac{1}{4}$个周期 | D． | 向右平移$\frac{1}{4}$个周期 |
16．已知复数z=2+i，则$\frac{\overline{z}}{z}$=（ ）
| A． | $\frac{3}{5}$-$\frac{4}{5}$i | B． | -$\frac{3}{5}$+$\frac{4}{5}$i | C． | $\frac{5}{3}$-$\frac{4}{3}$i | D． | -$\frac{5}{3}$+$\frac{4}{3}$i |
13．“方程f′（x）=0有解”是“函数y=f（x）有极值”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |