题目内容
12.已知函数f(x)=|x-1|-2|x+1|的最大值为k.(1)求k的值;
(2)若$\frac{1}{m}+\frac{1}{2n}=k({m>0,n>0})$,求证:m+2n≥2.
分析 (1)由已知可得f(x)=$\left\{\begin{array}{l}{-x-3,x≥1}\\{-3x-1,-1<x<1}\\{x+3,x≤-1}\end{array}\right.$,利用一次函数的单调性即可得出.
(2)由(1)可得:$\frac{1}{m}$+$\frac{1}{2n}$=2,(m,n>0).可得m+2n=$\frac{1}{2}$(m+2n)$(\frac{1}{m}+\frac{1}{2n})$=$\frac{1}{2}$(2+$\frac{2n}{m}$+$\frac{m}{2n}$),再利用基本不等式的性质即可得出.
解答 (1)解:∵f(x)=$\left\{\begin{array}{l}{-x-3,x≥1}\\{-3x-1,-1<x<1}\\{x+3,x≤-1}\end{array}\right.$,
∴f(x)的最大值为f(-1)=2,因此k=2.
(2)证明:由(1)可得:$\frac{1}{m}$+$\frac{1}{2n}$=2,(m,n>0).
∴m+2n=$\frac{1}{2}$(m+2n)$(\frac{1}{m}+\frac{1}{2n})$=$\frac{1}{2}$(2+$\frac{2n}{m}$+$\frac{m}{2n}$)≥1+$\frac{1}{2}×$2$\sqrt{\frac{2n}{m}•\frac{m}{2n}}$=2,当且仅当m=2n=1时取等号.
∴m+2n≥2.
点评 本题考查了绝对值不等式的性质、基本不等式的性质、一次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.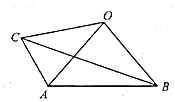 如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )
如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )
 如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )
如图,在四边形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ的值为( )| A. | $\frac{13}{6}$ | B. | $\frac{8}{3}$ | C. | $\frac{17}{6}$ | D. | $\frac{13}{3}$ |
20.已知i是虚数单位,则复数$z={({\frac{1+i}{{\sqrt{2}}}})^{2017}}$在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.在各项均为正数的等比数列{an}中,若anan+1=22n+1,则a5=( )
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
17.下列命题中的真命题为( )
| A. | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一的实数λ,使得$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |
| B. | 已知随机变量ξ服从正态分布N(1,σ2),若P(ξ≤4)=0.79,则P(ξ≤-2)=0.21 | |
| C. | “φ=$\frac{3π}{2}$”是“y=sin(2x+φ)为偶函数”的充要条件 | |
| D. | 函数y=f(1+x)与函数y=f(1-x)的图象关于直线x=1对称 |