题目内容
2.定义:函数f(x)在闭区间[a,b]上的最大值与最小值之差为函数f(x)的极差,若定义在区间[-2b,3b-1]上的函数f(x)=x3-ax2-(b+2)x是奇函数,则a+b=1,函数f(x)的极差为4.分析 由定义在区间[-2b,3b-1]上的函数f(x)=x3-ax2-(b+2)x是奇函数,列出方程组,能求出a=0,b=1,从而a+b=1,f(x)=x3-3x,由此利用导数的性质能求出函数f(x)的极差.
解答 解:∵定义在区间[-2b,3b-1]上的函数f(x)=x3-ax2-(b+2)x是奇函数,
∴$\left\{\begin{array}{l}{-2b+3b-1=0}\\{-a=0}\end{array}\right.$,解得a=0,b=1,∴a+b=1,
∴f(x)=x3-3x,区间[-2b,3b-1]即为[-2,2].
f′(x)=3x2-3,由f′(x)=0,得x=±1,
∵f(-2)=(-2)3-3×(-2)=-2,
f(-1)=(-1)3-3×(-1)=2,
f(1)=13-3×1=-2,
f(2)=23-3×2=2,
∴f(x)max=2,f(x)min=-2,
∴函数f(x)的极差为:2-(-2)=4.
故答案为:1,4.
点评 本题考查函数性质、函数极差、导数、函数最大值及最小值等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查数形结合思想,是中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
13.已知等比数列{an}的前n项和Sn=2n-a,则数列{log2an}的前10项和等于( )
| A. | 1023 | B. | 55 | C. | 45 | D. | 35 |
7.已知复数z=$\frac{2-i}{2+i}$-$\frac{2+i}{2-i}$,则z=( )
| A. | $\frac{6}{5}$i | B. | $\frac{8i}{5}$ | C. | -$\frac{8i}{5}$ | D. | -$\frac{6}{5}$i |
14.已知角φ的终边在射线$y=\sqrt{3}x(x≤0)$上,函数f(x)=cos(ωx+φ)(ω>0)图象的相邻两条对称轴之间的距离等于$\frac{π}{3}$,则$f(\frac{π}{6})$=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
19.直线$\left\{\begin{array}{l}x=1+tcosα\\ y=-2+tsinα\end{array}$(t为参数,0≤a<π)必过点( )
| A. | (1,-2) | B. | (-1,2) | C. | (-2,1) | D. | (2,-1) |
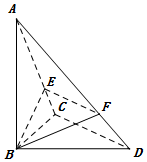 在三棱锥A-BCD中,AB⊥平面BCD,∠BCD=90°,E、F分别是AC、AD上的点,且$\frac{AE}{AC}=\frac{AF}{AD}$.
在三棱锥A-BCD中,AB⊥平面BCD,∠BCD=90°,E、F分别是AC、AD上的点,且$\frac{AE}{AC}=\frac{AF}{AD}$.