题目内容
7.在各项均为正数的等比数列{an}中,若anan+1=22n+1,则a5=( )| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
分析 令n=1,得到第1项与第2项的积为8,记作①,令n=2,得到第2项与第3项的积为32,记作②,然后利用②÷①,求出q的值,然后把q的值代入经过检验得到满足题意的q的值即可.
解答 解:各项均为正数的等比数列{an}中,
当n=1时,可得a1a2=8,当n=2时,a2a3=32,
相除可得 $\frac{{a}_{3}}{{a}_{1}}$=q2=4,q=±2.
当q=-2舍去.
∴公比q=2,a1a2=8,可得a1=2,
a5=32,
故选:32.
点评 此题考查学生掌握等比数列的性质,灵活运用等比数列的通项公式化简求值,是一道中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
18.有5件不同的商品,其中2件次品,3件正品,从中取出2件,至少有1件次品的概率为( )
| A. | $\frac{4}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
2.在区间$[{-\frac{5}{6},\frac{13}{6}}]$上随机取一个数x,则事件“$-1≤{log_{\frac{1}{3}}}({x+1})≤1$”不发生的概率为( )
| A. | $\frac{8}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
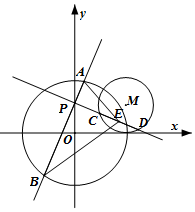 在平面直角坐标系xOy中,过点P(0,1)且互相垂直的两条直线分别与
在平面直角坐标系xOy中,过点P(0,1)且互相垂直的两条直线分别与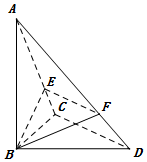 在三棱锥A-BCD中,AB⊥平面BCD,∠BCD=90°,E、F分别是AC、AD上的点,且$\frac{AE}{AC}=\frac{AF}{AD}$.
在三棱锥A-BCD中,AB⊥平面BCD,∠BCD=90°,E、F分别是AC、AD上的点,且$\frac{AE}{AC}=\frac{AF}{AD}$.