题目内容
甲、乙、丙三人互相传球,先由甲开始作第一次传球,则5次后球仍回到甲手中的不同传球方式有( )
| A、6 种 | B、8种 |
| C、10种 | D、16种 |
考点:计数原理的应用
专题:排列组合
分析:根据题意,设在第n次传球后(n≥2),有an种情况球在甲手中,由分步计数原理可得前n次传球的不同的传法共有2n种,进而可得球不在甲手中的情况有2n-an种情况,分析可得,只有在这些情况下,在下次传球时,球才会被传回甲,分析可得an+1=2n-an;易得a2=2,由递推公式,计算可得答案.
解答:
解:根据题意,设在第n次传球后(n≥2),有an种情况球在甲手中,
即经过n次传递后,球又被传回给甲,
而前n次传球中,每次传球都有2种方法,则前n次传球的不同的传球方法共有2n种,
那么在第n次传球后,球不在甲手中的情况有2n-an种情况,即球在乙或丙手中,
只有在这些情况时,在第n+1次传球后,球才会被传回甲,即an+1=2n-an;
易得a2=2,则a3=22-2=2,a4=23-2=6,a5=24-6=10,
故选:C.
即经过n次传递后,球又被传回给甲,
而前n次传球中,每次传球都有2种方法,则前n次传球的不同的传球方法共有2n种,
那么在第n次传球后,球不在甲手中的情况有2n-an种情况,即球在乙或丙手中,
只有在这些情况时,在第n+1次传球后,球才会被传回甲,即an+1=2n-an;
易得a2=2,则a3=22-2=2,a4=23-2=6,a5=24-6=10,
故选:C.
点评:本题考查了数列的应用,根据题意,分析发现第n次把球传回给甲(an)与第n次把球传回给甲(an+1)之间的关系,是解题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
在下列函数中,同时满足:①在(0,
)上递增;②以2π为周期;③是奇函数的是( )
| π |
| 2 |
| A、y=tanx | ||
| B、y=cosx | ||
C、y=tan
| ||
| D、y=-tanx |
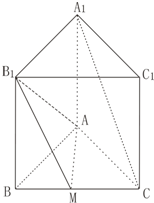 如图正三棱柱ABC-A1B1C1中底面边长AB=1,高BB1=1,M为底面BC边的中点.
如图正三棱柱ABC-A1B1C1中底面边长AB=1,高BB1=1,M为底面BC边的中点.