题目内容
已知cosα+sinβ=
,sinα+cosβ的取值范围是D,x∈D,则函数log
的最小值为 .
| 3 |
| 1 |
| 9 |
| ||
| 4x+7 |
考点:复合函数的单调性
专题:计算题,函数的性质及应用,三角函数的求值
分析:令t=sinα+cosβ,①cosα+sinβ=
,②,①2+②2,由平方关系和两角和的正弦公式及正弦函数的值域即可得到范围D,令y=
,则可运用导数求出区间D的单调性,即可得到y的最大值,从而由对数函数的单调性得到最小值.
| 3 |
| ||
| 4x+7 |
解答:
解:令t=sinα+cosβ,①
cosα+sinβ=
,②
①2+②2,得t2+3=2+2sin(α+β).
∴2sin(α+β)=t2+1∈[-2,2].
即t2+1≤2且t2+1≥-2,解得-1≤t≤1,
即有取值范围D为[-1,1],
由于x∈D,令y=
,则y=
=
≤
,
当且仅当2
=
,即有x=-
∉[-1,1],
故y取不到最大值
.
则函数的导数y′=
,在[-1,1]上y′<0,函数y是减函数,
则有x=-1,即y有最大值为
,
则函数log
的最小值为log
=
.
故答案为:
.
cosα+sinβ=
| 3 |
①2+②2,得t2+3=2+2sin(α+β).
∴2sin(α+β)=t2+1∈[-2,2].
即t2+1≤2且t2+1≥-2,解得-1≤t≤1,
即有取值范围D为[-1,1],
由于x∈D,令y=
| ||
| 4x+7 |
| ||
| 2(2x+3)+1 |
=
| 1 | ||||||
2
|
| 1 | ||
2
|
当且仅当2
| 2x+3 |
| 1 | ||
|
| 5 |
| 4 |
故y取不到最大值
| 1 | ||
2
|
则函数的导数y′=
| -4x-5 | ||
|
则有x=-1,即y有最大值为
| 1 |
| 3 |
则函数log
| 1 |
| 9 |
| ||
| 4x+7 |
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查三角函数的取值范围和复合函数的最值,考查三角恒等变换公式的运用,考查函数的单调性及运用,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
y=kx+k,y=
在同一坐标系中的图象大致是( )
| k |
| x |
A、 |
B、 |
C、 |
D、 |
表示如图中阴影部分所示平面区域的不等式组是( )
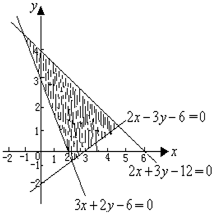

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|