题目内容
方程2x2-tx-t2=0在(-∞,-1)和(2,+∞)内各有一个实根,求t的取值范围.
考点:一元二次方程的根的分布与系数的关系
专题:计算题,函数的性质及应用
分析:化简方程2x2-tx-t2=(2x+t)(x-t)=0,从而求出根x=t或x=-
t,从而得不等式
或
,从而求出t的取值范围.
| 1 |
| 2 |
|
|
解答:
解:∵方程2x2-tx-t2=(2x+t)(x-t)=0
∴x=t或x=-
t,
∴
或
,
解得t>2或t<-4.
故t的取值范围为:t>2或t<-4.
∴x=t或x=-
| 1 |
| 2 |
∴
|
|
解得t>2或t<-4.
故t的取值范围为:t>2或t<-4.
点评:本题考查了方程的根的解法及根的范围问题,解出根,使根在区间内即可,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
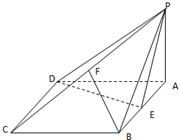 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.