题目内容
已知集合M={（x，y）|x2+y2≤25}，N={（x，y）|（x-a）2+y2≤9}，若M∪N=M，则a的取值范围为 ．
考点：圆与圆的位置关系及其判定
专题：直线与圆
分析：利用圆心距大于小于半径差，即可得到题目条件，求出a的范围．
解答：
解：集合M={（x，y）|x2+y2≤25}，表示（0，0）为圆心，半径为5的圆面，
N={（x，y）|（x-a）2+y2≤9}，表示（a，0）为圆心，半径为3的圆面，
M∪N=M，说明N在M的内部，即圆心距大于小于半径差，
可得：
≤5-3，解得-2≤a≤2．
故答案为：[-2，2]．
N={（x，y）|（x-a）2+y2≤9}，表示（a，0）为圆心，半径为3的圆面，
M∪N=M，说明N在M的内部，即圆心距大于小于半径差，
可得：
| (a-0)2 |
故答案为：[-2，2]．
点评：本题考查两个圆的位置关系，属于基本知识的考查．
练习册系列答案
相关题目
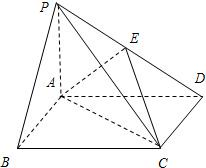如图，在底面是矩形的四棱锥P-ABCD中，PA⊥平面ABCD，PA=AB=2，BC=4．E是PD的中点，