题目内容
17.(文科)已知函数f(x)=2sin($\frac{1}{2}$x-$\frac{π}{6}$),x∈R(1)求它的振幅、周期和初相;
(2)求f($\frac{4π}{3}$)的值;
(3)求函数的最大值,最小值以及取得最大最小值时的x的取值;
(4)求它的增区间.
分析 利用正弦函数的图象与性质,即可得出结论.
解答 解:(1)∵函数f(x)=2sin($\frac{1}{2}$x-$\frac{π}{6}$),x∈R
∴振幅为2、周期为$\frac{2π}{\frac{1}{2}}$=4π,初相为-$\frac{π}{6}$;
(2)f($\frac{4π}{3}$)=2sin($\frac{2π}{3}$-$\frac{π}{6}$)=2;
(3)函数的最大值为2,$\frac{1}{2}$x-$\frac{π}{6}$=2kπ+$\frac{π}{2}$,可得x=4kπ+$\frac{4π}{3}$(k∈Z);
最小值为-2,$\frac{1}{2}$x-$\frac{π}{6}$=2kπ-$\frac{π}{2}$,可得x=4kπ-$\frac{2π}{3}$(k∈Z);
(4)由2kπ-$\frac{π}{2}$≤$\frac{1}{2}$x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,可得它的增区间为[4kπ-$\frac{2π}{3}$,4kπ+$\frac{4π}{3}$](k∈Z).
点评 本题考查正弦函数的图象与性质,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
2.已知z=2x+y,其中实数x,y满足$\left\{{\begin{array}{l}{y≥x}\\{x+y≤2}\\{x≥a}\end{array}}\right.$,且z的最大值是最小值的2倍,则a的值是( )
| A. | $\frac{2}{11}$ | B. | $\frac{1}{4}$ | C. | 4 | D. | $\frac{1}{2}$ |
9.已知等差数列{an}的前3项和为4,后3项和为7,所有项和为22,则项数n为( )
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
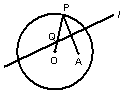 如图,圆O的半径为定长r,A是圆O内的一定点,P为圆上任意 一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆周上运动时,点Q的轨迹是( )
如图,圆O的半径为定长r,A是圆O内的一定点,P为圆上任意 一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆周上运动时,点Q的轨迹是( ) (1)某简单几何体的三视图中,正视图、侧视图、俯视图都是如图所示的直角边长为1的等腰直角三角形,求该几何体的表面积和体积;
(1)某简单几何体的三视图中,正视图、侧视图、俯视图都是如图所示的直角边长为1的等腰直角三角形,求该几何体的表面积和体积;