题目内容
一个容量为M的样本数据,其频率分布表如表.
(Ⅰ)完成频率分布表;
(Ⅱ)画出频率分布直方图;
(Ⅲ)利用频率分布直方图,估计总体的众数、中位数及平均数.
| 分组 | 频数 | 频率 |
| (10,20] | 2 | 0.10 |
| (20,30] | 3 | |
| (30,40] | 4 | 0.20 |
| (40,50] | ||
| (50,60] | 4 | 0.20 |
| (60,70] | 2 | 0.10 |
| 合计 | 1.00 |
(Ⅱ)画出频率分布直方图;
(Ⅲ)利用频率分布直方图,估计总体的众数、中位数及平均数.
考点:频率分布表,频率分布直方图,众数、中位数、平均数
专题:概率与统计
分析:(1)根据小组(10,20]的频数与频率,求出样本容量,再求出各小组对应的数据,补充完整频率分布表;
(2)根据频率分布表,画出频率分布直方图;
(3)根据频率分布直方图,求出众数、平均数与中位数.
(2)根据频率分布表,画出频率分布直方图;
(3)根据频率分布直方图,求出众数、平均数与中位数.
解答:
解:(1)在小组(10,20]中,频数是2,频率是0.10,∴样本数据为
=20;
∴小组(20,30]的频率为
=0.15;
小组(40,50]的频数为20-2-3-4-4-2=5,频率为
=0.25;
频数合计为20;
由此补充频率分布表如下:
(2)根据频率分布表,画出频率分布直方图如下:

(3)根据频率分布直方图,得;
图中最高的小矩形的底边中点坐标是
=45,∴众数为45;
平均数为
=15×0.1+25×0.15+35×0.20+45×0.25+55×0.20+65×0.10=41;
∵0.10+0.15+0.20=0.45<0.5,
0.45+0.25=0.70>0.5,
令0.45+0.25×
x=0.5,
解得x=2,∴中位数为40+2=42.
| 2 |
| 0.1 |
∴小组(20,30]的频率为
| 3 |
| 20 |
小组(40,50]的频数为20-2-3-4-4-2=5,频率为
| 5 |
| 20 |
频数合计为20;
由此补充频率分布表如下:
| 分组 | 频数 | 频率 |
| (10,20] | 2 | 0.10 |
| (20,30] | 3 | 0.15 |
| (30,40] | 4 | 0.20 |
| (40,50] | 5 | 0.25 |
| (50,60] | 4 | 0.20 |
| (60,70] | 2 | 0.10 |
| 合计 | 20 | 1.00 |

(3)根据频率分布直方图,得;
图中最高的小矩形的底边中点坐标是
| 40+50 |
| 2 |
平均数为
. |
| x |
∵0.10+0.15+0.20=0.45<0.5,
0.45+0.25=0.70>0.5,
令0.45+0.25×
| 1 |
| 10 |
解得x=2,∴中位数为40+2=42.
点评:本题考查了频率分布直方图的应用问题,解题时应利用分布直方图进行有关的运算,是基础题目.

练习册系列答案
相关题目
设如图是某几何体的三视图,则该几何体的体积为( )
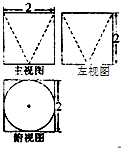

A、
| ||
B、8-
| ||
| C、8-2π | ||
D、8-
|
设平面向量
=(-1,0),
=(0,2),则2
+3
等于( )
| a |
| b |
| a |
| b |
| A、(6,3) |
| B、(-2,6) |
| C、(2,1) |
| D、(7,2) |